| |
die Symmetriegruppen von Kristallstrukturen. Die Elemente einer Raumgruppe sind die isometrischen (abstandstreuen) Abbildungen einer Kristallstruktur auf sich, wobei die Verknüpfung zweier Abbildungen als deren Hintereinanderausführen definiert ist. Die Raumgruppe einer n-dimensionalen Kristallstruktur wird eine n-dimensionale Raumgruppe genannt. Wegen des periodischen Aufbaus einer Kristallstruktur befinden unter den Symmetrieoperationen einer Raumgruppe stets Translationen (Verschiebungen). Diese Translationen bilden eine Untergruppe der Raumgruppe, und zwar einen Normalteiler. Die Faktorgruppe der Raumgruppe nach dem Translationen-Normalteiler ist isomorph zu einer kristallographischen Punktgruppe. Man kann die Bildung der Faktorgruppe und damit den Übergang von der Raumgruppe zur Punktgruppe als eine Projektion auffassen, bei der die Translationen zum Wegfall kommen. Über die Punktgruppe ist die Raumgruppe damit einer Kristallklasse und über die Kristallklasse einem Kristallsystem eindeutig zugeordnet.
Zur Bezeichnung der Raumgruppen werden heute fast ausschliesslich die Hermann-Mauguin-Symbole (internationale Symbole) verwendet. Es sind sowohl sog. vollständige Symbole wie P2/m2/n21/a als auch gekürzte Symbole wie Pmna in Gebrauch, wobei bei den Raumgruppen einiger Kristallklassen die beiden Symbole zusammenfallen. Die erste Stelle wird von einem Buchstaben eingenommen, der (zusammen mit der Information über das Kristallsystem, das sich aus dem weiteren Teil des Symbols ergibt) das Bravais-Gitter und damit die Translationen der Raumgruppe charakterisiert. Die weiteren Zeichen bezeichnen Symmetrieoperationen, die - je nach Stellung im Symbol - verschiedenen Raumrichtungen zugeordnet sind. Tab. 1 gibt einen kurzen überblick über die Symmetrieoperationen der dreidimensionalen Raumgruppen. Unter der Zähligkeit einer Drehung oder Drehinversion wird die Ordnung der Symmetrieoperation verstanden, d.h. die Anzahl der Anwendungen bis zur Erreichung der Ausgangslage. Eine p-zählige Drehung bzw. Drehinversion um eine Achse erfolgt gegen den Uhrzeigersinn, wenn der Betrachter in Richtung auf den Ursprung blickt. Damit führt z.B. eine Schraubung 41 zu einer Rechtsschraube, 43 zu einer Linksschraube. Die Bezugsrichtungen für die 2., 3. und 4. Stelle sind in Tab. 2angegeben. Bei manchen Raumgruppen bleiben die letzten beiden Stellen oder die letzte Stelle unbesetzt. Man kann die Angaben im Raumgruppensymbol als Erzeugende der Raumgruppe auffassen. Hierzu werde als Beispiel wieder P2/m2/n21/a, kurz Pmna, betrachtet (in welcher Raumgruppe, neben einigen anderen Strukturen, der Eriochalcit, CuCl2·2H2O, kristallisiert). Das Symbol der zugehörigen Kristallklasse findet man durch Löschen aller Information über die Translationen: P2/m2/n21/a→2/m2/m2/m, kurz mmm. Das ist eine der drei Kristallklassen des orthorhombischen Kristallsystems. Die Bestandteile des Raumgruppensymbols sind (in der Reihenfolge von links nach rechts) dann wie folgt zu interpretieren:
P: Primitives orthorhombisches Translationsgitter, welches von drei Translationen τ( 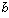
), τ( 
) und τ(
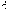 ) mit Translationsvektoren ) mit Translationsvektoren 
und 
bzw.

erzeugt werden kann,
2: eine 2-zählige Drehung um eine Achse parallel zu 
,
m: eine Spiegelung an einer Ebene senkrecht zu 
,
2: eine 2-zählige Drehung um eine Achse parallel zu 
,
n: eine Gleitspiegelung mit Verschiebungsvektor ( 
+ 
)/2 an einer Ebene senkrecht zu 
,
21: eine 2-zählige Schraubung um eine Achse parallel zu 
,
a: eine Gleitspiegelung mit Verschiebungsvektor 
/2 an einer Ebene senkrecht zu 
.
Zur Erzeugung der Raumgruppe genügen auch die Operationen, die sich aus dem kurzen Symbol Pmna ablesen lassen, also die drei Translationen und die drei Spiegelungen bzw. Gleitspiegelungen, und selbst die Menge dieser sechs Abbildungen bildet kein Minimalsystem von Erzeugenden, denn die Translationen τ( 
) und τ( 
) lassen sich aus den verbleibenden Elementen als τ( 
)=a2 und τ( -1
 )=n2·a erzeugen. Insgesamt gibt es 230 Raumgruppen des dreidimensionalen Raums. Eine besonders einfache Struktur haben die 73 symmorphen Raumgruppen, in denen sich jede Symmetrieoperation als Produkt einer Translation und einer Drehung oder Drehinversion darstellen lässt. Sie sind daran erkenntlich, dass auf den an der ersten Stelle stehenden Buchstaben ein Kristallklassen-Symbol folgt. )=n2·a erzeugen. Insgesamt gibt es 230 Raumgruppen des dreidimensionalen Raums. Eine besonders einfache Struktur haben die 73 symmorphen Raumgruppen, in denen sich jede Symmetrieoperation als Produkt einer Translation und einer Drehung oder Drehinversion darstellen lässt. Sie sind daran erkenntlich, dass auf den an der ersten Stelle stehenden Buchstaben ein Kristallklassen-Symbol folgt.
Für kristallographische Berechnungen bedient man sich der Matrizen einer Matrix-Darstellung der betreffenden Raumgruppe, wobei man sich zunutze macht, dass sich die isometrischen Abbildungen des dreidimensionalen Raums durch 4×4-Matrizen darstellen lassen. Hierzu ein Beispiel: Bezogen auf das für die Raumgruppe Pmna üblicherweise gewählte Koordinatensystem lässt sich die Abbildung eines Punktes mit Koordinaten x, y, z durch eine n-Gleitspiegelung wie folgt darstellen:
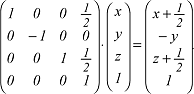 Die jeweils letzten Zeilen dienen dem Formalismus und sind bei allen Matrizen gleich. Aus den Die jeweils letzten Zeilen dienen dem Formalismus und sind bei allen Matrizen gleich. Aus den
Koordinaten x+1/2, -y, z+1/2 des Bildpunkts, hier als Zeile geschrieben, lassen sich die Elemente der
Matrix rekonstruieren. Damit kann die Angabe der Bildkoordinaten die voluminöse Matrix-Schreibweise ersetzen. In der kristallographischen Literatur ist es üblich, das Minuszeichen
nicht vor, sondern über die entsprechende Zahl zu setzen, womit die Bildkoordinaten als x+1/2, z+1/2 zu schreiben sind. Als eine abgekürzte Matrix-Schreibweise lässt sich die Seitz-Notation
auffassen. Hier werden die ersten drei Zeilen und Spalten der 4×4-Matrix durch einen Grossbuchstaben und die drei ersten Elemente der letzten Spalte durch einen Kleinbuchstaben
dargestellt, und zwar in der Form (W,w), zuweilen auch als (W|w). Mit Hilfe der Matrix-Multiplikation
verifiziert man leicht, dass (W,w)·(U,u)=(WU, Wu+w) und (W,w)-1=(W-1, -W-1w).
Die Definition des Begriffs »Raumgruppe« gilt für Räume beliebiger Dimension. Neben den bisher diskutierten dreidimensionalen Raumgruppen seien erwähnt: a) eindimensionale Raumgruppen: Hier
gibt es zwei Raumgruppen als Symmetriegruppen der beiden Muster:
·· · ·· · ·· · ·· ·
und · · · · · · · · · · · ·.
b) zweidimensionale Raumgruppen (Ebenengruppen) und c) vier- und höherdimensionale
Raumgruppen; die Raumgruppen der fünf- und höherdimensionalen Räume sind nur partiell bekannt.
Wenn von 230 Raumgruppen im dreidimensionalen Raum die Rede ist, dann ist diese
Bezeichnungsweise zu präzisieren. Verschiedene Kristallstrukturen, die beispielweise die Symmetrie
Pmna aufweisen, werden sich durch ihre Gitterparameter und damit durch die Beträge der
Translationsvektoren ihrer Raumgruppen unterscheiden. Allgemein gilt: Eine Raumgruppe ist die
Symmetriegruppe einer ganz speziellen Kristallstruktur, und da man sich unendlich viele
verschiedene Kristallstrukturen vorstellen kann, so gibt es entsprechend unendlich viele
Raumgruppen, die nach bestimmten Merkmalen zu klassifizieren sind. Die wichtigsten
Klassifikationskriterien sind a) affine Äquivalenz: Zwei Raumgruppen R und R‘ heissen affin äquivalent, wenn es eine affine Abbildung α gibt, so dass α-1Rα=R‘. b) positiv affine Äquivalenz: zwei
Raumgruppen R und R‘ heissen positiv affin äquivalent, wenn es eine affine Abbildung α+ mit positiver
Determinante gibt, so dass (α+)-1R(α+)=R‘. c) Isomorphie: Zwei Raumgruppen R und R‘ heissen isomorph, wenn sie als abstrakte Gruppen isomorph sind. Tab. 3 enthält die Ergebnisse der
Klassifikation der Raumgruppen im ein-, zwei-, drei- und vierdimensionalen Raum. Der Unterschied
zwischen positiv affiner und affiner Äquivalenz besteht darin, dass enantiomorphe Paare von
Raumgruppen (wie z.B. die Raumgruppen von Rechtsquarz und Linksquarz) in der erstgenannten
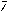 Klassifikation unterschieden werden, in der zweiten hingegen nicht. Dass die Klasseneinteilungen nach affiner Äquivalenz und Isomorphie zu denselben Ergebnissen führen, ist kein Zufall, sondern gilt allgemein nach einem Satz von Bieberbach. Die übliche Einteilung ist diejenige nach positiv affiner Äquivalenz. Sie führt zu den sogenannten Raumgruppentypen. Klassifikation unterschieden werden, in der zweiten hingegen nicht. Dass die Klasseneinteilungen nach affiner Äquivalenz und Isomorphie zu denselben Ergebnissen führen, ist kein Zufall, sondern gilt allgemein nach einem Satz von Bieberbach. Die übliche Einteilung ist diejenige nach positiv affiner Äquivalenz. Sie führt zu den sogenannten Raumgruppentypen.
Die 230 Typen von dreidimensionalen Raumgruppen wurden um das Jahr 1890 sowohl von dem Mineralogen und Kristallographen E.S. Fedorov in St. Petersburg als auch von dem Mathematiker A. Schoenflies in Göttingen, zunächst unabhängig voneinander, dann in der Endphase in einem Briefwechsel stehend, erstmals abgeleitet. Literatur: [1] Brown, H., Bülow, R., Neubüser, J., Wondratschek, H. und Zassenhaus, H. (1978): Crystallographic Groups of Four-Dimensional Space. - New York. [2] Hahn, Th. (Hrsg.) (1992): International Tables for Crystallography, Volume A, Space-Group Symmetry. - Dordrecht.
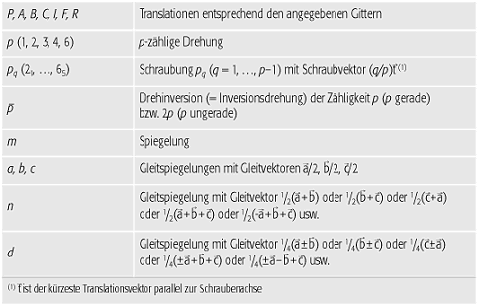 Raumgruppen (Tab. 1): Raumgruppenoperationen im dreidimensionalen Raum. Raumgruppen (Tab. 1): Raumgruppenoperationen im dreidimensionalen Raum.
 Raumgruppen (Tab 2): dreidimensionale Raumgruppen (Bezugsrichtungen für die Symmetrieoperationen in den Hermann-Mauguin-Symbolen). Raumgruppen (Tab 2): dreidimensionale Raumgruppen (Bezugsrichtungen für die Symmetrieoperationen in den Hermann-Mauguin-Symbolen).
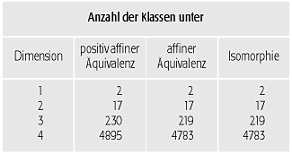 Raumgruppen (Tab. 3): Klassifikation der Raumgruppen. Raumgruppen (Tab. 3): Klassifikation der Raumgruppen. |
|