| |
einer quadratischen Matrix M wird durch die folgende Formel eine Zahl zugeordnet, die als Determinante von
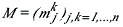 bezeichnet wird: bezeichnet wird:
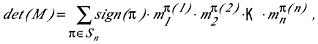 wobei sich die Summe über alle n! Permutationen von (1,2,...,n) erstreckt. Dabei ist sign(π)= +1 für gerade und -1 für ungerade Permutationen. Gerade heisst eine Permutation, wenn sie durch eine gerade Zahl von Vertauschungen (Transpositionen) je zweier Elemente aus der Grundform (1,2,...,n) hervorgeht. Die einfachsten Fälle sind: wobei sich die Summe über alle n! Permutationen von (1,2,...,n) erstreckt. Dabei ist sign(π)= +1 für gerade und -1 für ungerade Permutationen. Gerade heisst eine Permutation, wenn sie durch eine gerade Zahl von Vertauschungen (Transpositionen) je zweier Elemente aus der Grundform (1,2,...,n) hervorgeht. Die einfachsten Fälle sind:
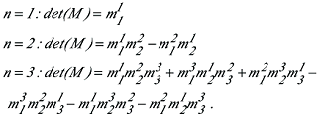 Beschreibt die Matrix eine Basistransformation, indem die Spalten die Koordinaten der neuen Basisvektoren bezüglich der alten Basis angeben, so zeigt die Determinante die Volumenänderung des von den drei Basisvektoren aufgespannten Parallelepipeds (Spats) an. Aus diesem Grund tritt auch der Betrag der Funktionaldeterminante bei Integraltransformationen in Erscheinung. Bei der Verwendung der Matrizen zur Beschreibung von linearen Transformationen ist die Determinante eine Invariante der Transformation (unter Basistransformationen des zugrundeliegenden Raumes). Die Determinante des Metriktensors gibt das Volumenquadrat des Spats (Elementarzelle) an. Beschreibt die Matrix eine Basistransformation, indem die Spalten die Koordinaten der neuen Basisvektoren bezüglich der alten Basis angeben, so zeigt die Determinante die Volumenänderung des von den drei Basisvektoren aufgespannten Parallelepipeds (Spats) an. Aus diesem Grund tritt auch der Betrag der Funktionaldeterminante bei Integraltransformationen in Erscheinung. Bei der Verwendung der Matrizen zur Beschreibung von linearen Transformationen ist die Determinante eine Invariante der Transformation (unter Basistransformationen des zugrundeliegenden Raumes). Die Determinante des Metriktensors gibt das Volumenquadrat des Spats (Elementarzelle) an. |
|