| |
stellen eine Beziehung zwischen der durch eine mechanische Spannung verursachten Verformung (Sijkl, elastische Module) bzw. zwischen der Verformung und der daraus resultierenden mechanischen Spannung (Cijkl, elastische Konstanten) her. Die durch einen Tensor vierter Stufe beschriebenen elastischen Eigenschaften gelten nur für den Fall, dass mechanische Spannung und elastische Verformung zueinander proportional sind (Hookesches Gesetz). Ausserhalb der Gültigkeit des Hookeschen Gesetzes sind für die Beschreibung der elastischen Eigenschaften Tensoren höherer Ordnung (6. Stufe, 8. Stufe,...) notwendig (Abb. 1). Die maximal 36 unabhängigen Koeffizienten des s-und c-Tensors reduzieren sich für isotrope Festkörper auf zwei und werden durch verschiedene elastische Module und elastische Konstanten beschrieben (Tab. 1). Sind zwei unabhängige elastische Eigenschaften eines isotropen Festkörpers bestimmt, lassen sich die anderen elastischen Grössen mathematisch ableiten (Tab. 2).
Die elastischen Grössen lassen sich aus statischen Experimenten bestimmen. Messtechnisch sind die aus entsprechenden Experimenten gewonnen elastischen Grössen mit einem relativ grossen Fehler behaftet. Die Untersuchung der elastischen Eigenschaften erfolgt deshalb heute überwiegend mit dynamischen Methoden (Schallgeschwindigkeiten, Brillouin-Spektroskopie). In anisotropen Festkörpern werden zur vollständigen Beschreibung der elastischen Eigenschaften bis zu 21 unabhängige Komponenten benötigt. Der entsprechende Tensor vierter Stufe lässt sich im zweidimensionalen nur unbefriedigend darstellen (3×3×3×3-Matrix). Voigt (1928) schlug deshalb die heute verbreitete Darstellung der elastischen Eigenschaften in einer 6×6-Matrix vor. Mit den Umrechnungsvorschriften können die Tensorkomponenten cijkl (sijkl) und Matrixkomponenten Cij (Sij) umgewandelt werden. Die resultierenden Matrizen sind symmetrisch und es gilt Cij = Cji bzw. Sij = Sji (Tab. 3). Eine Schallwelle pflanzt sich durch die Deformation einzelner Bereiche in einem Festkörper fort. Die Fortpflanzungsgeschwindigkeit hängt von den elastischen Eigenschaften und der Dichte ρ des Körpers ab. Für isotrope Festkörper werden zwei unterschiedliche Schallgeschwindigkeiten beobachtet, eine longitudinale und eine transversale Schallwelle (seismische Wellen). Im isotropen Medium sind bei Kompressionswellen (longitudinale Schallwellen) Ausbreitungsrichtung und Verzerrungsvektor parallel zueinander, während bei einer Scherwelle (transversale Welle) Ausbreitungsrichtung und Verzerrungsvektor in einem Winkel von 90° zueinander stehen. Scherwellen sind demnach polarisierte Schallwellen, während die longitudinalen Schallwellen nicht polarisiert sind. Für isotrope Festkörper lassen sich die Schallgeschwindigkeiten, aus den elastischen Eigenschaften und der Dichte, gemäss folgender Beziehungen berechnen (Gebrande):
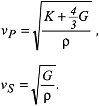 Für anisotrope Festkörper können die elastischen Eigenschaften ebenfalls aus Messungen der Schallgeschwindigkeiten bestimmt werden. Aus den elastodynamischen Grundgleichungen folgt für die Ausbreitungsgeschwindigkeit v einer Schallwelle (ebene Welle) unter Annahme der Gültigkeit des Hookeschen Gesetzes: Für anisotrope Festkörper können die elastischen Eigenschaften ebenfalls aus Messungen der Schallgeschwindigkeiten bestimmt werden. Aus den elastodynamischen Grundgleichungen folgt für die Ausbreitungsgeschwindigkeit v einer Schallwelle (ebene Welle) unter Annahme der Gültigkeit des Hookeschen Gesetzes:
-ρv
0.
2δik+cijklgjgl)ξk = Trifft eine Scherwelle auf einen anisotropen Körper, so werden im allgemeinen Fall - wenn die Polarität der eingestrahlten Schallwelle keinen Bezug zu den Polarisationsrichtungen des Festkörpers in dieser Richtung hat - zwei Scherwellen mit unterschiedlicher Schallgeschwindigkeit den Körper durchschallen (ähnlich der optischen Doppelbrechung). In Abbildung 2 ist die Aufspaltung einer Schallwelle (shear-wave-splitting) dargestellt. In ausgezeichneten Richtungen und in isotropen Medien werden nur zwei Schallwellen (Entartung) beobachtet (vP und vs). In Festkörpern werden mindestens zwei Schallwellen beobachtet. Je nach Kristallklasse müssen bis zu 36 verschiedene Koeffizienten bestimmt werden, um die elastischen Eigenschaften vollständig zu beschreiben. In vielen Kristallklassen reduziert sich die Anzahl der unabhängigen Komponenten. Die elastischen Eigenschaften eines Kristalls können als Ergebnis der Wechselwirkungen (Bindungen) von Atomen betrachtet werden. Für die Beschreibung der Bindungsverhältnisse reicht im Bereich der Gültigkeit des Hookeschen Gesetzes die Annahme eines Potentials aus, welches durch eine quadratische lineare Gleichung beschrieben wird. Bei grösseren mechanischen Spannungen, Druck- oder Temperaturänderungen müssen für die Beschreibung der beobachteten elastischen Eigenschaften die Asymmetrie des Potentials berücksichtigt werden. Die elastischen Eigenschaften werden damit vom Druck und der Temperatur abhängig. Die Druckabhängigkeit des Kompressionsmoduls K wird oft über eine Birch-Murnaghan-Gleichung beschrieben:
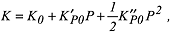 wobei K0, KP0 ' und KP0'' Konstanten darstellen. Eine entsprechende Reihenentwicklung kann auch für die Temperaturabhängigkeit verwendet werden: wobei K0, KP0 ' und KP0'' Konstanten darstellen. Eine entsprechende Reihenentwicklung kann auch für die Temperaturabhängigkeit verwendet werden:
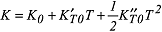 mit den Kostanten K0, KT0 ' und KT0''. Ähnliche Reihenentwicklungen können auch für die anderen Module angewandt werden. Die aus den elastischen Eigenschaften abgeleiteten Schallgeschwindigkeiten zeigen ein ähnliches Verhalten (Abb. 3). Druck und Temperatur wirken auf die Schallgeschwindigkeiten in entgegengesetzter Richtung. Führt eine Druckzunahme zu einer Erhöhung der Schallgeschwindigkeit, so führt eine Erwärmung der Minerale zu einer Geschwindigkeitserniedrigung. Eine Ausnahme stellt dabei die S-Wellengeschwindigkeit von Quarz dar. Die bei Mineralen beobachtete Änderung der elastischen Module mit der Temperatur führt bei Gesteinen auch zu einer Abnahme der intrinsischen Schallgeschwindigkeiten (Abb. 5). Werden Gesteinseigenschaften bei höheren Drücken und Temperaturen untersucht, muss der Einfluss des Gefüges und des Mikrogefüges auf die elastischen Eigenschaften berücksichtigt werden. So ändert sich das elastische Verhalten (Schallgeschwindigkeit) von Gesteinen durch das Schliessen von Mikrorissen und Poren (Porenraum) oft deutlich (Abb. 4). mit den Kostanten K0, KT0 ' und KT0''. Ähnliche Reihenentwicklungen können auch für die anderen Module angewandt werden. Die aus den elastischen Eigenschaften abgeleiteten Schallgeschwindigkeiten zeigen ein ähnliches Verhalten (Abb. 3). Druck und Temperatur wirken auf die Schallgeschwindigkeiten in entgegengesetzter Richtung. Führt eine Druckzunahme zu einer Erhöhung der Schallgeschwindigkeit, so führt eine Erwärmung der Minerale zu einer Geschwindigkeitserniedrigung. Eine Ausnahme stellt dabei die S-Wellengeschwindigkeit von Quarz dar. Die bei Mineralen beobachtete Änderung der elastischen Module mit der Temperatur führt bei Gesteinen auch zu einer Abnahme der intrinsischen Schallgeschwindigkeiten (Abb. 5). Werden Gesteinseigenschaften bei höheren Drücken und Temperaturen untersucht, muss der Einfluss des Gefüges und des Mikrogefüges auf die elastischen Eigenschaften berücksichtigt werden. So ändert sich das elastische Verhalten (Schallgeschwindigkeit) von Gesteinen durch das Schliessen von Mikrorissen und Poren (Porenraum) oft deutlich (Abb. 4).
Die meisten Gesteine zeigen eine Zunahme der Schallgeschwindigkeiten mit der Dichte. Auch innerhalb einzelner Gesteinsarten (z.B. Sandsteine) wird eine Zunahme der Schallgeschwindigkeit mit der Dichte beobachtet. Oft wird eine Dichte-Geschwindigkeits-Relation - auch Birch-Law genannt - zur Interpretation seismischer Beobachtungen verwendet. Der Zusammenhang zwischen Geschwindigkeit und Dichte ist in Abb. 6 schematisch dargestellt. Für detailierte Studien muss die Porosität, das Gefüge, der Druck und die Temperatur sowie die chemische Zusammensetzung der Gesteine berücksichtigt werden (Petrophysik, Mineralphysik).
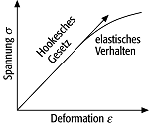 elastische Eigenschaften 1: Hookesches Gesetz: linearer Zusammenhang zwischen mechanischer Spannung σ und Deformation � (Dehnungsexperiment). elastische Eigenschaften 1: Hookesches Gesetz: linearer Zusammenhang zwischen mechanischer Spannung σ und Deformation � (Dehnungsexperiment).
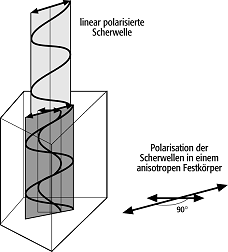 elastische Eigenschaften 2: Aufspaltung einer Scherwelle beim Eintritt in einen anisotropen Festkörper (shear-wave-splitting). elastische Eigenschaften 2: Aufspaltung einer Scherwelle beim Eintritt in einen anisotropen Festkörper (shear-wave-splitting).
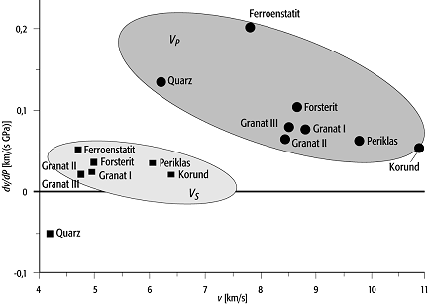 elastische Eigenschaften 3: Änderung der mittleren Schallgeschwindigkeiten von Mineralen mit dem Druck. Die P-Wellen-Geschwindigkeiten sind durch Kreise, die S-Wellen-Geschwindigkeiten durch Rechtecke dargestellt. elastische Eigenschaften 3: Änderung der mittleren Schallgeschwindigkeiten von Mineralen mit dem Druck. Die P-Wellen-Geschwindigkeiten sind durch Kreise, die S-Wellen-Geschwindigkeiten durch Rechtecke dargestellt.
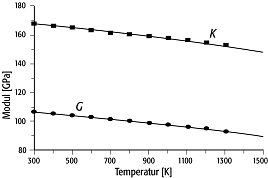 elastische Eigenschaften 4: Änderung der elastischen Module mit der Temperatur für einen Grossular (Granat). elastische Eigenschaften 4: Änderung der elastischen Module mit der Temperatur für einen Grossular (Granat).
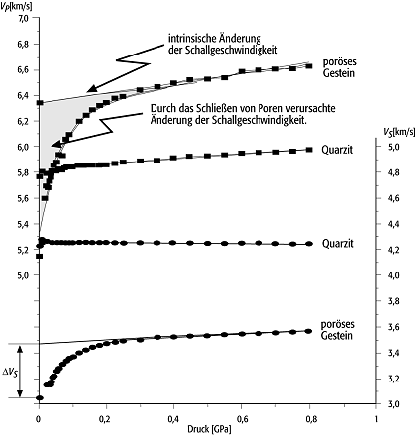 elastische Eigenschaften 5: Schallgeschwindigkeiten als Funktion des Druckes für Gesteine (quadratische Symbole repräsentieren gemessene P-, runde Symbole S-Wellen-Geschwindigkeiten; die durchgezogenen Geraden deuten das intrinsische Verhalten an, welches durch die Änderung der Schallgeschwindigkeit der Minerale verursacht wird). elastische Eigenschaften 5: Schallgeschwindigkeiten als Funktion des Druckes für Gesteine (quadratische Symbole repräsentieren gemessene P-, runde Symbole S-Wellen-Geschwindigkeiten; die durchgezogenen Geraden deuten das intrinsische Verhalten an, welches durch die Änderung der Schallgeschwindigkeit der Minerale verursacht wird).
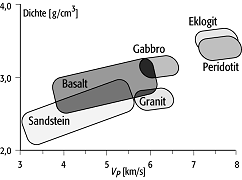 elastische Eigenschaften 6: schematische Darstellung der Änderung der Geschwindigkeit mit der Dichte für einige Gesteine. elastische Eigenschaften 6: schematische Darstellung der Änderung der Geschwindigkeit mit der Dichte für einige Gesteine.
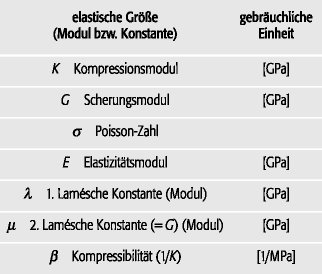 elastische Eigenschaften (Tab. 1): elastische Module und Konstanten zur Beschreibung des elastischen Verhaltens isotroper Körper. elastische Eigenschaften (Tab. 1): elastische Module und Konstanten zur Beschreibung des elastischen Verhaltens isotroper Körper.
 elastische Eigenschaften (Tab. 2): Verknüpfungen zwischen verschiedenen elastischen Grössen für isotrope Medien. elastische Eigenschaften (Tab. 2): Verknüpfungen zwischen verschiedenen elastischen Grössen für isotrope Medien.
 elastische Eigenschaften (Tab. 3): Umrechnung eines s- bzw. c-Tensors in eine Matrix. elastische Eigenschaften (Tab. 3): Umrechnung eines s- bzw. c-Tensors in eine Matrix. |
|