| |
Kraft pro Flächeneinheit. Spannungen wirken in einem Festkörper, der einer Kraft ausgesetzt ist. Die in einem Körper wirkende Spannung kann einen materialspezifischen maximalen Grenzwert nicht überschreiten, der als Festigkeitbezeichnet wird. Die Festigkeit geologischer Körper ist abhängig von der vorherrschenden Temperatur, vom Umlagerungsdruck bzw. von der aufgezwungenen Verformungsrate. Bei Überschreiten seiner Festigkeit erfolgt im Gestein ein Spannungsabfall,der mit mechanischem Versagen und irreversibler, bleibenden Verformung verbunden ist. Beim Kraftansatz an einer Fläche eines Körpers wirken zwei Spannungskomponenten: die Normalspannung(σn) normal zur Fläche und die Scherspannung(τ) parallel zur Fläche.
Normalspannungen können als positive Druckspannungen (Kompression) oder negative Zugspannungen (Tension) auftreten. Als Masseinheit der Spannung dient das Pascal (Pa) = 1 N/m2. Für jeden Punkt innerhalb eines Körpers kann man sich eine unendliche Zahl von Flächenlagen vorstellen. Bei einem Kraftansatz von aussen wirken entlang jeder dieser Flächen Normal- und Scherspannungen. Die Gesamtheit dieser Spannungen an einem Punkt bezeichnet man als den Spannungszustandan diesem Punkt. Der Spannungszustand für ein infinitesimal kleines Körperelement lässt sich mathematisch als dreidimensionaler Spannungstensormit drei Normal- und sechs Scherspannungskomponenten darstellen. Es gibt allerdings eine einzige räumliche Orientierung des infinitesimal kleinen Kubus, bei welcher die Scherspannungen gleich Null sind. In diesem Fall wird der Spannungstensor allein durch die drei Normalspannungen definiert, die als Hauptnormalspannungen σ1 >σ2 >σ3 bezeichnet werden. Graphisch wird der Spannungstensor als Spannungsellipsoid(Abb. 1)illustriert, also durch Grösse und Orientierung der Ellipsoidachsen σ1, σ2 und σ3. Normal- und Scherspannung werden häufig mit der Konstruktion des Mohrschen Spannungskreises als Funktion von σ1, σ2 und σ3 dargestellt (Abb. 2). Aus dieser Konstruktion ergibt sich bei zweidimensionaler Betrachtung in der σ1-σ3-Ebene:
σn=(σ1+σ2)/2 + (σ1-σ3)/2 cos2α und τ=(σ1-σ3)/2 sin2α,
wobei α den Winkel zwischen σ1 und der Normalen der betrachteten Fläche bezeichnet. Von besonderer Bedeutung dafür, ob irreversible Verformungen erzeugt werden, ist die Spannungsdifferenz (Differentialspannung) σ1-σ3. Von ihr, vom Umlagerungsdruck und vom Porenfluiddruck hängt es ab, ob ein Material permanent oder elastisch-reversibel verformt wird.
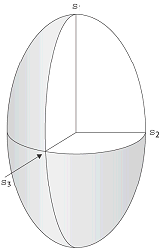 Spannung 1: Spannungsellipsoid der Hauptnormalspannungen σ1 >σ2 >σ3. Spannung 1: Spannungsellipsoid der Hauptnormalspannungen σ1 >σ2 >σ3.
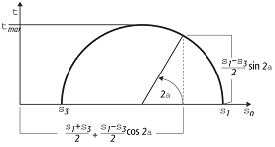 Spannung 2: Mohrscher Spannungskreis zur Bestimmung der Scher- (τ) und Normalspannung (σn) aus den Hauptnormalspannungen σ1 und σ3 sowie des Winkels α zwischen der Flächennormalen und σ1. Spannung 2: Mohrscher Spannungskreis zur Bestimmung der Scher- (τ) und Normalspannung (σn) aus den Hauptnormalspannungen σ1 und σ3 sowie des Winkels α zwischen der Flächennormalen und σ1. |
|