| |
elastische Dehnung, elastische Verformung, linear elastische Reaktion eines Körpers auf z.B. eine einwirkende Spannung, eine Temperaturänderung, ein angelegtes elektrisches Feld (reziproker Piezoeffekt) oder ein magnetisches Feld (Magnetostriktion). Für einen isotropen, d.h. einen in allen Raumrichtungen sich gleich verhaltenden Körper reichen zur Beschreibung des elastischen Verhaltens zwei Kenngrössen aus. Dies ist zum einen der Elastizitätsmodul E, welcher über das Hookesche Gesetz σ = E� (σ entspricht einer Zug- oder Druckspannung in den Einheiten Pa = N/m2, E dem Elastizitätsmodul in Pa und � der Dehnung, d.h. der relativen Längenänderung Δl/l) eine linear aufgebrachte Spannung mit der ebenfalls dann linear auftretenden Dehnung verknüpft. Zum anderen benötigt man eine zweite Grösse, den Torsionsmodul G, der den Widerstand eines Körpers gegen eine Scherspannung τ beschreibt. In diesem Fall gilt: τ = Gα mit dem Torsionswinkel α. Die Querkontraktion, d.h. die relative Änderung des Durchmessers,
z.B. eines unter Zugbelastung stehenden Stabes, im Verhältnis zur relativen Längenänderung, wird durch die Poisson-Zahl ν beschrieben. Diese verknüpft den Elastizitäts- mit dem Torsionsmodul über:
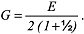 Wegen der anisotropen elastischen Eigenschaften von Einkristallen ist deren elastisches Verhalten komplizierter. Im allgemeinen muss sowohl der Spannungszustand σkl als auch der Dehnungszustand �ij durch einen polaren Tensor zweiter Stufe beschrieben werden. Hierbei entsprechen die σkk (�ii) den Normalspannungen (Dehnungen) und die σk≠l (�i≠j) den Scherspannungen (Scherungen). Beide Tensoren sind symmetrisch, d.h. σkl = σlk bzw. �ij = �ji und besitzen demnach je sechs unabhängige Grössen. Der Spannungstensor ist über den Tensor vierter Stufe der Elastizitätsmodule cijkl mit dem Dehnungstensor verknüpft: Wegen der anisotropen elastischen Eigenschaften von Einkristallen ist deren elastisches Verhalten komplizierter. Im allgemeinen muss sowohl der Spannungszustand σkl als auch der Dehnungszustand �ij durch einen polaren Tensor zweiter Stufe beschrieben werden. Hierbei entsprechen die σkk (�ii) den Normalspannungen (Dehnungen) und die σk≠l (�i≠j) den Scherspannungen (Scherungen). Beide Tensoren sind symmetrisch, d.h. σkl = σlk bzw. �ij = �ji und besitzen demnach je sechs unabhängige Grössen. Der Spannungstensor ist über den Tensor vierter Stufe der Elastizitätsmodule cijkl mit dem Dehnungstensor verknüpft:
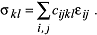 Der Tensor cijkl besteht aus 34=81 Koeffizienten. Diese Anzahl reduziert sich wegen der Symmetrie des Spannungs- und Dehnungstensors auf 36. Durch eine Umindizierung der jeweils sechs unabhängigen Koeffizienten von σkl und �ij nach σm und �n mit m,n =1...6 und der entsprechenden Umindizierung der cijkl nach cmn ergibt sich die Gleichung: Der Tensor cijkl besteht aus 34=81 Koeffizienten. Diese Anzahl reduziert sich wegen der Symmetrie des Spannungs- und Dehnungstensors auf 36. Durch eine Umindizierung der jeweils sechs unabhängigen Koeffizienten von σkl und �ij nach σm und �n mit m,n =1...6 und der entsprechenden Umindizierung der cijkl nach cmn ergibt sich die Gleichung:
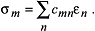 Die Indizes m =1...3 beziehen sich dabei auf die Normalspannungen und m =4...6 auf die Scherspannungen. Entsprechendes gilt auch für die Dehnungen und Scherungen. Diese anschauliche, auch in Matrixschreibweise darstellbare Form der Gleichung geht auf Voigt zurück. Durch die Betrachtung der Deformationsenergie lässt sich weiterhin zeigen, dass cnm = . Damitcmnverringert sich die Anzahl der unabhängigen Parameter von 36 auf 21. Dies ist exakt die Anzahl freier Parameter, die für die vollständige Beschreibung des elastischen Verhaltens eines triklinen Kristalls notwendig ist. Mit höherer Symmetrie erniedrigt sich diese Zahl weiter (Tab.). Selbst für kubische Kristalle werden noch drei Parameter benötigt. Dies ist ein Parameter mehr als bei vollständiger Isotropie der elastischen Eigenschaften. Die Abweichung des Elastizitätsmoduls vom isotropen Verhalten lässt sich durch sog. Elastizitätsmodulkörper veranschaulichen. So wie bisher die Spannung als Funktion der Dehnung betrachtet wurde, kann dies auch umgekehrt werden: Die Indizes m =1...3 beziehen sich dabei auf die Normalspannungen und m =4...6 auf die Scherspannungen. Entsprechendes gilt auch für die Dehnungen und Scherungen. Diese anschauliche, auch in Matrixschreibweise darstellbare Form der Gleichung geht auf Voigt zurück. Durch die Betrachtung der Deformationsenergie lässt sich weiterhin zeigen, dass cnm = . Damitcmnverringert sich die Anzahl der unabhängigen Parameter von 36 auf 21. Dies ist exakt die Anzahl freier Parameter, die für die vollständige Beschreibung des elastischen Verhaltens eines triklinen Kristalls notwendig ist. Mit höherer Symmetrie erniedrigt sich diese Zahl weiter (Tab.). Selbst für kubische Kristalle werden noch drei Parameter benötigt. Dies ist ein Parameter mehr als bei vollständiger Isotropie der elastischen Eigenschaften. Die Abweichung des Elastizitätsmoduls vom isotropen Verhalten lässt sich durch sog. Elastizitätsmodulkörper veranschaulichen. So wie bisher die Spannung als Funktion der Dehnung betrachtet wurde, kann dies auch umgekehrt werden:
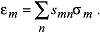 Die Grössen smn (elastische Konstanten) stellen ebenfalls einen Tensor vierter Stufe mit maximal 21 unabhängigen Koeffizienten dar. Die Grössen smn (elastische Konstanten) stellen ebenfalls einen Tensor vierter Stufe mit maximal 21 unabhängigen Koeffizienten dar.
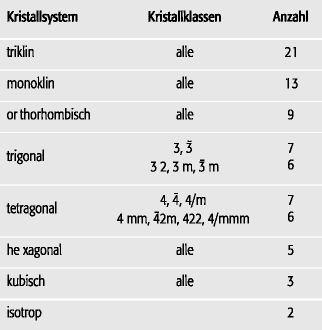 elastische Deformation (Tab): Anzahl der unabhängigen elastischen Koeffizienten für die verschiedenen Kristallklassen. elastische Deformation (Tab): Anzahl der unabhängigen elastischen Koeffizienten für die verschiedenen Kristallklassen. |
|