| |
orthogonale Matrix zur Drehung zweier beliebiger aber gleichsinnig orientierter rechtwinkliger Dreibeine. Eine allgemeine Drehung kann in unterschiedlicher Weise aus aufeinander folgenden Teildrehungen um drei Achsen zusammengesetzt werden. Im Falle grosser Drehungen ist dabei zu beachten, in welcher Reihenfolge die Teildrehungen ausgeführt werden. Das Kommutativgesetz gilt somit nicht für grosse Drehungen, wohl aber für kleine Drehwinkel. Setzt man eine Gesamtdrehung aus Teildrehungen um Achsen des jeweils momentanen Dreibeines zusammen, so sind drei Elementardrehungen um die drei möglichen Achsen des rechtwinkligen Dreibeines, wie in der Tabelle angegeben, zu unterscheiden. Die positive Zählrichtung erfolgt dabei gegen den Uhrzeigersinn.
Für die Drehung der Basiseinheitsvektoren des Koordinatensystems zwei in die Basiseinheitsvektoren des Koordinatensystems eins gilt beispielsweise:
 mit der Drehmatrix
D(ψ,θ,φ)= D3(φ)D1(θ)D3(ψ).
Für die inverse Drehung gilt wegen der Orthogonalitätseigenschaft der Drehmatrizen:
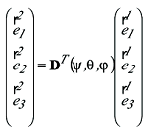 mit der transponierten Matrix:
DT(ψ,θ,φ)= D3T(ψ)D1T(θ)D3T(φ)
Entsprechend erhält man für die Transformation der Koordinaten der gedrehten Koordinatensysteme:
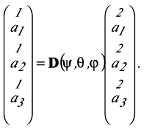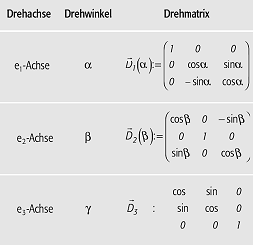  Drehmatrix (Tab.): Elementardrehungen eines rechtsgerichteten Dreibeines. |
|
