|
| |
|
| |
Lagenkugelprojektion |
|
| |
|
|
| |
Projektionsmethode, mit der die Verteilung geologischer Datenmengen in einer Ebene auf der Lagenkugel dargestellt wird. Grundsätzlich sind hierfür alle in der Kartographie üblichen Methoden, die Erdoberfläche in einer zweidimensionalen Projektion darzustellen, möglich. Es haben sich jedoch zwei Methoden in der Geologie und in der Kristallographie besonders bewährt: die stereographische Projektion und die Lambertsche Projektion.
a) Die stereographische Projektion ist eine Zentralprojektion, bei der der Zenith der Vollkugel das Projektionszentrum und die Äquatorebene die Projektionsebene bilden (Abb. 1). In der Praxis wird ein Netz, das Wulffsche Netz (Abb. 2), in dem Längen- und Breitenkreise nach der stereographischen Projektion abgeleitet sind, verwendet, um Richtungsdaten manuell in eine stereographische Projektion einzutragen. Dieses Netz hat den Vorteil, dass auch in der Projektion Längen- und Breitenkreise einen rechten Winkel miteinander bilden, man sagt, dieses Netz ist winkeltreu, während gleiche Flächen auf der Kugeloberfläche in der Projektion mit unterschiedlicher Grösse dargestellt werden. Wegen der Winkeltreue lassen sich geometrische Konstruktionen besser mit diesem Netz ausführen. In der Kristallographie lassen sich mit Hilfe des Wulffschen Netzes Messwerte von Flächenpolen am Reflexionsgoniometer leicht in die stereographische Projektion übertragen, wenn man den Mittelpunkt des Wulffschen Netzes von unten mit einem Reissnagel durchsticht, ein Blatt Transparentpapier damit aufspiesst und die Ausgangslage durch einen Strich beim Winkel φ=0º markiert. Dreht man dann das aufgelegte Blatt im Uhrzeigersinn um den Messwinkel φ, so kann man vom Mittelpunkt aus auf der Geraden des Wulffschen Netzes, die die Nullmarkierung trägt, den Messwinkel ρ (Poldistanz) abtragen. Man erhält so für alle Messwerte (ρ,φ) den entsprechenden Punkt in der stereographischen Projektion. Längs der Grosskreise des Wulffschen Netzes lassen sich Winkeldistanzen messen. Ausserdem kann man durch Drehen des Deckblatts je zwei Flächenpole auf einen Grosskreis bringen und so den gemeinsamen Zonenkreis (Zone) finden.
b) Die Lambertsche Projektion wurde von dem Philosophen und Mathematiker J.H. Lambert (1728-1777) für die flächentreue Abbildung der Erdoberfläche entwickelt und wird heute häufig in der Geographie verwendet. Sie stellt keine Projektion im mathematischen Sinne dar (Abb. 3). Die Projektionsebene liegt unter der Lagenkugel, d.h. sie ist die Tangentialebene im Nadir an die Kugel. Ein Netz, in dem Längen- und Breitengrade in dieser "Projektion" dargestellt werden, heisst Schmidtsches Netz. Es ist flächentreu und eignet sich deshalb für den Vergleich grösserer Datenmengen und deren statistische Auswertung (Abb. 4a, Abb. 4b). Im Paläomagnetismus werden die Richtungen der remanenten Magnetisierung und auch die virtuellen geomagnetischen Pole (VGP) generell im Schmidtschen Netz in einer flächentreuen Projektion dargestellt. Man kennt sowohl äquatorständige als auch polständige Schmidtsche Netze. Für die Darstellung der Remanenzrichtungen verwendet man i.d.R. die polständige Version. Nach einer Konvention werden die Richtungen mit einer positiven Inklination mit geschlossenen, diejenigen mit einer ne-gativen Inklination mit offenen Symbolen gezeigt. Für die Darstellung von Pollagen verwendet man auch häufig äquator-ständige Projektionen sowie Projektionen aus beliebigen Richtungen oder sogar Merkatorprojektionen, um möglichst viele Pole auf einer Hemisphäre darstellen zu können. Pole auf der Nordhalbkugel werden dann mit geschlossenen, Pole auf der Südhalbkugel mit offenen Symbolen gekennzeichnet. Gefügediagramm.
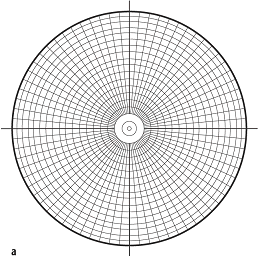 Lagenkugelprojektion 4a: a) flächentreue (Lambertsche) Polarprojektion der Lagenkugel. Lagenkugelprojektion 4a: a) flächentreue (Lambertsche) Polarprojektion der Lagenkugel.
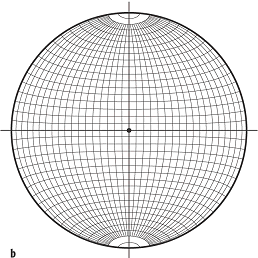 Lagenkugelprojektion 4b: b) flächenreue Azimutalprojektion der Lagenkugel (Schmidtsches Netz). Lagenkugelprojektion 1: Prinzip der stereographischen Projektion ( Lagenkugelprojektion 4b: b) flächenreue Azimutalprojektion der Lagenkugel (Schmidtsches Netz). Lagenkugelprojektion 1: Prinzip der stereographischen Projektion ( 
= lineares Element, K = Berührungspunkt des linearen
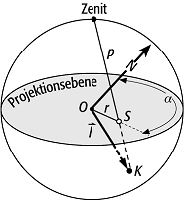 Elementes mit der unteren Halbkugel, S = Projektionspunkt von K in der Projektionsebene, α = Azimut von Elementes mit der unteren Halbkugel, S = Projektionspunkt von K in der Projektionsebene, α = Azimut von 
, r = Strecke = Funktion des Fallwinkels).
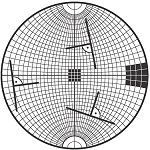 Lagenkugelprojektion 2: Wulffsches Netz. Die Seiten der schwarzen Flächen entsprechen einem Bogen von 20º auf der Kugeloberfläche. Lagenkugelprojektion 2: Wulffsches Netz. Die Seiten der schwarzen Flächen entsprechen einem Bogen von 20º auf der Kugeloberfläche.
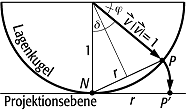 Lagenkugelprojektion 3: die Lambertsche Projektion. Der Berührungspunkt P eines linearen Elementes v mit der Lagenkugel wird durch einen Kreisbogen um den Nadir N mit dem Radius NP in den Punkt P' überführt (r = Strecke = Funktion des Fallwinkels, δ = Hilfswinkel, φ = Fallwinkel). Lagenkugelprojektion 3: die Lambertsche Projektion. Der Berührungspunkt P eines linearen Elementes v mit der Lagenkugel wird durch einen Kreisbogen um den Nadir N mit dem Radius NP in den Punkt P' überführt (r = Strecke = Funktion des Fallwinkels, δ = Hilfswinkel, φ = Fallwinkel). |
|
| |
|
|
| |
Ein Bookmark auf diese Seite setzen:
|
|
| |
|
|
| |
<< vorheriger Begriff |
|
nächster Begriff >> |
|
|
|
|
|
| |
|
|
|
|