| |
thermische Dilatation, 1) Geophysik: kann durch die Anharmonizität atomarer Schwingungen erklärt werden. Sie beruht auf der Änderung der mittleren Schwerpunktslage der Bausteine. Es wird meist eine Zunahme der thermischen Ausdehnungskoeffizienten mit zunehmender Temperatur beobachtet, als Folge der mit steigender Temperatur wachsenden Amplitude thermischer Schwingungen. Die Temperaturabhängigkeit der thermischen Ausdehnung kann als Änderung der Anharmonizität der atomaren Schwingungen mit zunehmender Temperatur beschrieben werden. Zur Beschreibung der thermischen Ausdehnungskoeffizienten als Funktion der Temperatur werden meist lineare Gleichungen der Form:
a·x+bx2+c/x... verwendet. Die Druckabhängigkeit der thermischen Ausdehnung ergibt sich aus der Änderung der Kompressibilität mit der Temperatur. Bei Gesteinen kann die intrinsische thermische Ausdehnung aus den Mineraleigenschaften abgeleitet werden. Die thermische Ausdehnung der Gesteine wird durch eingeschlossene Poren nur unwesentlich beeinflusst, sofern die Kompressibilität der Porenfüllung wesentlich grösser als die der Matrix ist (z.B. gasgefüllte Poren oder Flüssigkeitseinschlüsse). Bei thermischen Ereignissen kann sich die Anzahl der Poren und das Porenvolumen in der Probe ändern. Einen erheblichen Einfluss auf das Gefüge können Mineralreaktionen und Umwandlungen haben. Diese können, wie z.B. die α/β-Quarzumwandlung, durch eine starke Volumenänderung zu Rissen führen. (Abb.). Lineare thermische Ausdehnung beschreibt das Ausdehnungsverhalten in einer vorgegebenen Richtung. Der thermische Ausdehnungskoeffizient αlin [1/K] ist definiert als die Änderung der Probenlänge δl durch eine infinitisimale Temperaturerhöhung δT:
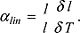 In der Technik ist der technische Ausdehnungskoeffizient αtech [1/K] üblich, der die Längenänderung (Δl) auf die Normalbedingungen bezieht: In der Technik ist der technische Ausdehnungskoeffizient αtech [1/K] üblich, der die Längenänderung (Δl) auf die Normalbedingungen bezieht:
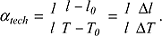 Die lineare thermische Ausdehnung ist i.a. eine anisotrope Eigenschaft (Anisotropie) und kann durch Die lineare thermische Ausdehnung ist i.a. eine anisotrope Eigenschaft (Anisotropie) und kann durch
einen Tensor 2. Stufe beschrieben werden (Tab. 1).
Die thermische Volumendehnung αvol [1/K] ergibt sich aus der Volumenänderung δV der Probe durch
eine Temperaturänderung:
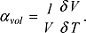 In erster Näherung gilt für isotrope Körper αvol ≈ 3αlin. Die Volumenausdehnung der meisten Gesteine liegt im Bereich von 30·10-6/K (Tab. 2). 2) Mineralogie: oft eher unzutreffend als Wärmeausdehnung bezeichneter Begriff für die relativ auf die Koordinatenachsen bezogene Längenänderung durch eine Temperaturänderung ΔT. Für einen dünnen Stab der Länge l0 erhält man in erster Näherung: In erster Näherung gilt für isotrope Körper αvol ≈ 3αlin. Die Volumenausdehnung der meisten Gesteine liegt im Bereich von 30·10-6/K (Tab. 2). 2) Mineralogie: oft eher unzutreffend als Wärmeausdehnung bezeichneter Begriff für die relativ auf die Koordinatenachsen bezogene Längenänderung durch eine Temperaturänderung ΔT. Für einen dünnen Stab der Länge l0 erhält man in erster Näherung:
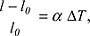 dabei bezeichnet α den linearen Ausdehnungskoeffizienten. Für Kristalle hängt der Ausdehnungskoeffizient von der Richtung ab, in der der Stab aus dem Kristall herausgeschnitten worden ist. Die physikalische Eigenschaft der thermischen Ausdehnung muss daher durch einen symmetrischen Tensor 2. Stufe, αij beschrieben werden. Der Zustand der Dehnung des Kristalls wird selbst durch einen aus physikalischen Gründen symmetrischen Tensor 2. Stufe, den Dehnungstensor �ij (elastische Deformation), dargestellt. Die obige Gleichung für die richtungsabhängige thermische Ausdehnung in Kristallen muss daher wie folgt formuliert werden: dabei bezeichnet α den linearen Ausdehnungskoeffizienten. Für Kristalle hängt der Ausdehnungskoeffizient von der Richtung ab, in der der Stab aus dem Kristall herausgeschnitten worden ist. Die physikalische Eigenschaft der thermischen Ausdehnung muss daher durch einen symmetrischen Tensor 2. Stufe, αij beschrieben werden. Der Zustand der Dehnung des Kristalls wird selbst durch einen aus physikalischen Gründen symmetrischen Tensor 2. Stufe, den Dehnungstensor �ij (elastische Deformation), dargestellt. Die obige Gleichung für die richtungsabhängige thermische Ausdehnung in Kristallen muss daher wie folgt formuliert werden:
�ij=αij(ΔT)+βij(ΔT)2+...; i,j=1,2,3.
In einem kleinen Temperaturintervall von einigen Grad Kelvin genügt es normalerweise, die linearen Ausdehnungskoeffizienten αij heranzuziehen, wenn die Ausdehnung mit einer Genauigkeit von 1% erfasst werden soll. Ansonsten müssen die Koeffizienten höherer Ordnung βij hinzugenommen werden. Die richtungsabhängige thermische Ausdehnung in Kristallen kann sehr leicht augenfällig demonstriert werden. Man erwärmt eine aus einem nicht kubischen Kristall geschliffene Kugel. Sie verformt sich zu einem Rotationsellipsoid oder zu einem allgemeinen Ellipsoid, je nach der Symmetrie des Kristalls. Die Koeffizienten in den Hauptachsen des Ellipsoids, das sind die Koeffizienten αii in der Hauptdiagonale der 3×3-Matrix (αij), nennt man Hauptausdehnungskoeffizienten. In der Geologie ist die thermische Ausdehnung bei der physikalischen Verwitterung der Gesteine durch Sonneneinstrahlung sowie auch für die künstliche Gesteinszerstörung von Bedeutung. thermische Eigenschaften.
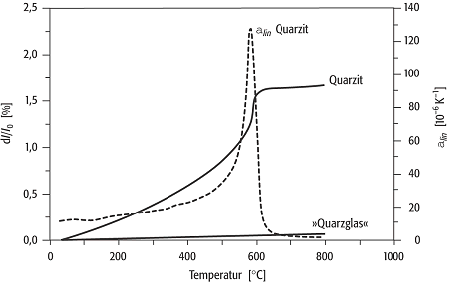 thermische Ausdehnung: thermische Ausdehnung von Quarzit und „Quarzglas” (SiO2-Glas). Die durchgezogene Linie stellt die relative Längenänderung (dl/l0), die gestrichelte Linie den linearen thermischen Ausdehnungskoeffizienten (αlin) dar. thermische Ausdehnung: thermische Ausdehnung von Quarzit und „Quarzglas” (SiO2-Glas). Die durchgezogene Linie stellt die relative Längenänderung (dl/l0), die gestrichelte Linie den linearen thermischen Ausdehnungskoeffizienten (αlin) dar.
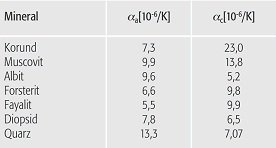 thermische Ausdehnung (Tab. 1): anisotrope thermische Ausdehnungskoeffizienten in orthogonalen Richtungen (parallel und senkrecht zu den grössten und kleinsten Ausdehnungskoeffizienten. thermische Ausdehnung (Tab. 1): anisotrope thermische Ausdehnungskoeffizienten in orthogonalen Richtungen (parallel und senkrecht zu den grössten und kleinsten Ausdehnungskoeffizienten.
 |
|