| |
Fläche zweiter Ordnung, die durch Drehung einer abgeplatteten Meridianellipse um die kleine Halbachse entsteht. a) Geometrische Parameter der Meridianellipse: Die Form der Meridianellipse wird durch die grosse Halbachse a und die kleine Halbachse b beschrieben. Sie definieren die Formparameter des Rotationsellipsoids. Als zweiter geometrischer Parameter wird häufig statt der kleinen Halbachse b die geometrische Abplattung f, die lineare Exzentrizität E oder die erste numerische Exzentrizität e bzw. die zweite numerische Exzentrizität e‘ verwendet. Wichtige Parameter des Rotationsellipsoids sind in der Tabelle zusammengestellt (Abb. 1 und 2). Wegen des geringen Unterschiedes der Achsen des Rotationsellipsoids als Approximation für die Figur der Erde (a-b ≈ 21 km) sind diese Grössen klein und für Reihenentwicklungen besser geeignet. b) Parameterdarstellung des Rotationsellipsoids: Das Rotationsellipsoid erhält man aus der Rotation der Meridianellipse. Die Mittelpunktsgleichung des Rotationsellipsoids lautet:
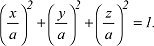 Mit dem Parallelkreishalbmesser p (L ist die ellipsoidische Länge), Mit dem Parallelkreishalbmesser p (L ist die ellipsoidische Länge),
x=p cosL, y=p sinL
lautet die Mittelpunktsgleichung:
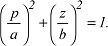 Die Grössen p und z können als Funktionen der ellipsoidischen (geodätischen) Breite B dargestellt werden: Die Grössen p und z können als Funktionen der ellipsoidischen (geodätischen) Breite B dargestellt werden:
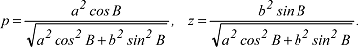 Legt man die in der Landesvermessung üblichen Abkürzungen Legt man die in der Landesvermessung üblichen Abkürzungen
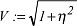 mit mit
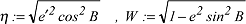 zugrunde, so ergeben sich dafür die kompakteren Formeln: zugrunde, so ergeben sich dafür die kompakteren Formeln:
p=NcosB, z=(N/1+e‘2)sinB
mit dem Querkrümmungsradius N:
N:=c/V=a/W
und dem Meridiankrümmungsradius M in einem Punkt P mit der Breite B:
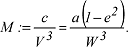 In Abhängigkeit von der reduzierten Breite β können die Grössen p und z ausgedrückt werden: In Abhängigkeit von der reduzierten Breite β können die Grössen p und z ausgedrückt werden:
p=acosβ, z=bsinβ
und als Funktion der geozentrischen Breite γ:
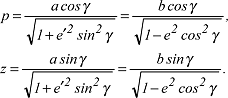 Die Parameterdarstellung des Rotationsellipsoids lautet in Abhängigkeit von der ellipsoidischen Breite B: x=NcosBcosL, y=NcosBsinL, Die Parameterdarstellung des Rotationsellipsoids lautet in Abhängigkeit von der ellipsoidischen Breite B: x=NcosBcosL, y=NcosBsinL,
z=N/1+e‘2sinB.
Entsprechend erhält man die Darstellungen in Abhängigkeit von der reduzierten Breite β:
x=acosβcosL,
y=acosβsinL,
z=bsinβ
bzw. in Abhängigkeit von der geozentrischen Breite γ:
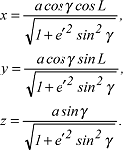 Diese Gleichungen beziehen sich auf ein Koordinatensystem mit dem Ursprung im Mittelpunkt des Rotationsellipsoids und einer Achsenorientierung im Sinne eines konventionellen geodätischen Koordinatensystems. Bezogen auf ein lokales ellipsoidisches Koordinatensystem mit dem Ursprung in einem Ellipsoidpunkt P1 erhält man für die Gleichung des Rotationsellipsoids: Diese Gleichungen beziehen sich auf ein Koordinatensystem mit dem Ursprung im Mittelpunkt des Rotationsellipsoids und einer Achsenorientierung im Sinne eines konventionellen geodätischen Koordinatensystems. Bezogen auf ein lokales ellipsoidisches Koordinatensystem mit dem Ursprung in einem Ellipsoidpunkt P1 erhält man für die Gleichung des Rotationsellipsoids:
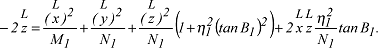 c) Krümmung des Rotationsellipsoids: Die Meridiane und Parallelkreise des Rotationsellipsoids sind die Krümmungslinien des Rotationsellipsoids. Die Hauptkrümmungsradien liegen somit in der Meridianebene (Meridiankrümmungsradius M) und in der dazu senkrechten Normalebene (Querkrümmungsradius N). Damit folgt der Gausssche Krümmungsradius als positive Quadratwurzel aus dem Kehrwert des Gaussschen Krümmungsmasses: c) Krümmung des Rotationsellipsoids: Die Meridiane und Parallelkreise des Rotationsellipsoids sind die Krümmungslinien des Rotationsellipsoids. Die Hauptkrümmungsradien liegen somit in der Meridianebene (Meridiankrümmungsradius M) und in der dazu senkrechten Normalebene (Querkrümmungsradius N). Damit folgt der Gausssche Krümmungsradius als positive Quadratwurzel aus dem Kehrwert des Gaussschen Krümmungsmasses:
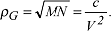 Die Abhängigkeit der Normalkrümmung einer Flächenkurve in Abhängigkeit vom ellipsoidischen Azimut α ergibt sich nach der Formel von Euler: Die Abhängigkeit der Normalkrümmung einer Flächenkurve in Abhängigkeit vom ellipsoidischen Azimut α ergibt sich nach der Formel von Euler:
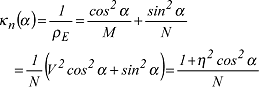 mit dem Eulerschen Krümmungsradius ρE. Die geodätische Torsion einer Flächenkurve in Abhängigkeit vom Azimut erhält man aus der Formel: mit dem Eulerschen Krümmungsradius ρE. Die geodätische Torsion einer Flächenkurve in Abhängigkeit vom Azimut erhält man aus der Formel:
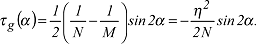 Für die Kurvenkrümmung eines Parallelkreises gilt: Für die Kurvenkrümmung eines Parallelkreises gilt:
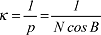 sowie für die Normalkrümmung eines Parallelkreises: κn=1/N. Die geodätische Krümmung eines sowie für die Normalkrümmung eines Parallelkreises: κn=1/N. Die geodätische Krümmung eines
Parallelkreises erhält man aus:
κg=1/(NcotB).
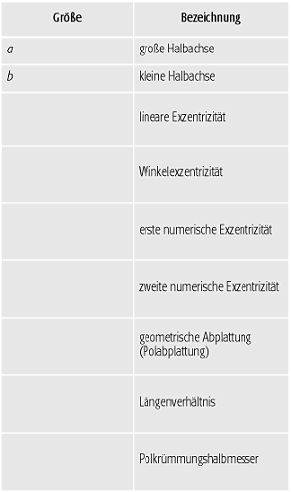 Rotationsellipsoid (Tab.): Parameter des Rotationsellipsoids. Rotationsellipsoid 1: geometrische Parameter des Rotationsellipsoids. Rotationsellipsoid (Tab.): Parameter des Rotationsellipsoids. Rotationsellipsoid 1: geometrische Parameter des Rotationsellipsoids.
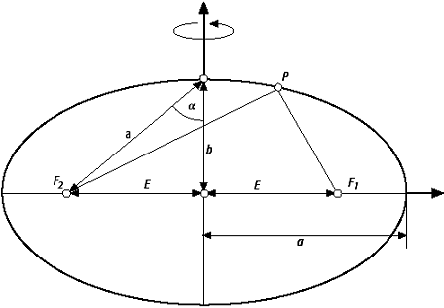
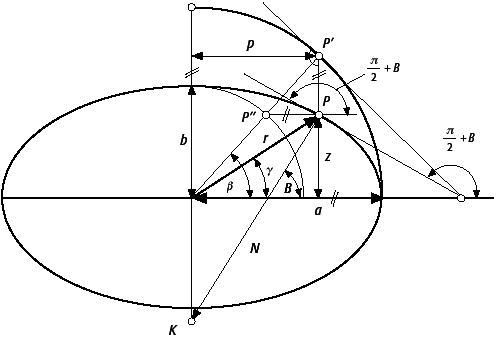 Rotationsellipsoid 2: Geometrie der Meridianellipse. Rotationsellipsoid 2: Geometrie der Meridianellipse. |
|