| |
Verhältnis vf der Grösse einer differentiellen Fläche auf der Kugel als Bezugsfläche zur entsprechenden differentiellen Fläche in der Kartenebene als Abbildungsfläche. Praktikabler als die Formeln der Verzerrungstheorie zur Berechnung der Flächenverzerrung sind Formeln, die das Flächenverhältnis mit Hilfe verschiedener Längenverzerrungsausdrücke ergeben. In der Abbildung 1 ist oben ein differentielles sphärisches Dreieck in der Bezugsfläche und unten seine Abbildung in der Ebene dargestellt. dS, dSm und dSp sind die differentiellen Bogenstücke zwischen den Punkten P1, P2 und P3. Die mit einem Strich versehenen Stücke und Punkte sind die Entsprechungen in der Ebene, wobei der rechte Winkel bei P2 in den Winkel θ bei P2 ' verzerrt wird. Aus dem Verhältnis der differentiellen Flächen auf der Kugel und in der Ebene ergibt sich unter Anwendung der Formel für die Dreiecksfläche:
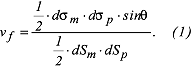 Nach der Verzerrungstheorie, Gleichungen (8) und (10), gilt für die Längenverzerrung im Meridian mm und im Parallel mp: Nach der Verzerrungstheorie, Gleichungen (8) und (10), gilt für die Längenverzerrung im Meridian mm und im Parallel mp:
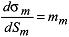 und und
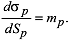 Damit erhält die Gleichung (1) die einfache Form vf = mm ·mp·sinθ. (2) Damit erhält die Gleichung (1) die einfache Form vf = mm ·mp·sinθ. (2)
Unter Verwendung der Fundamentalgrössen der Gaussschen Flächentheorie (Verzerrungstheorie) gilt:
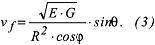 Für unecht kegelige Kartennetzentwürfe gilt θ≠90°. Setzt man in (2) für mm und mp die aus der Verzerrungstheorie bekannten Ausdrücke (8) und (10) und für sinθ die aus der Verzerrungstheorie Gleichung (41) durch Umformung von tanθ erhaltene Beziehung ein, so hat man für den allgemeinen Fall der Flächenverzerrung: Für unecht kegelige Kartennetzentwürfe gilt θ≠90°. Setzt man in (2) für mm und mp die aus der Verzerrungstheorie bekannten Ausdrücke (8) und (10) und für sinθ die aus der Verzerrungstheorie Gleichung (41) durch Umformung von tanθ erhaltene Beziehung ein, so hat man für den allgemeinen Fall der Flächenverzerrung:
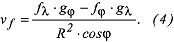 Darin sind fφ, fλ, gφ und gλ die partiellen Ableitungen der Funktionen f(φ,λ) und g(φ,λ) in den allgemeinen Abbildungsgleichungen. Für alle echt kegeligen, aber auch für einige unecht kegeligen Kartennetzentwürfe in normaler Abbildung (in polarer Lage der Kegelachse) gilt θ = 90° (Winkelverzerrung Gleichung (13)). Die Rechtschnittigkeit zwischen Meridianen und Parallelkreisen auf der Kugel bleibt also in der Abbildung erhalten. In diesem Fall wird die Flächenverzerrung mit den Ausdrücken (19) der Verzerrungstheorie so errechnet: Darin sind fφ, fλ, gφ und gλ die partiellen Ableitungen der Funktionen f(φ,λ) und g(φ,λ) in den allgemeinen Abbildungsgleichungen. Für alle echt kegeligen, aber auch für einige unecht kegeligen Kartennetzentwürfe in normaler Abbildung (in polarer Lage der Kegelachse) gilt θ = 90° (Winkelverzerrung Gleichung (13)). Die Rechtschnittigkeit zwischen Meridianen und Parallelkreisen auf der Kugel bleibt also in der Abbildung erhalten. In diesem Fall wird die Flächenverzerrung mit den Ausdrücken (19) der Verzerrungstheorie so errechnet:
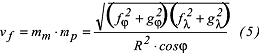 oder mit den Fundamentalgrössen (Verzerrungstheorie Gleichung (6)): oder mit den Fundamentalgrössen (Verzerrungstheorie Gleichung (6)):
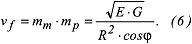 Erheblichen Flächenverzerrungen unterliegen winkeltreue Kartennetzentwürfe an den Rändern des dargestellten Gebietes. Das trifft besonders für die Abbildung sehr grosser Teile des Globus in die Ebene zu. Erheblichen Flächenverzerrungen unterliegen winkeltreue Kartennetzentwürfe an den Rändern des dargestellten Gebietes. Das trifft besonders für die Abbildung sehr grosser Teile des Globus in die Ebene zu.
Eine Vorstellung von der Flächenverzerrung der quadratischen Plattkarte, einem Zylinderentwurf, vermitteln die Tissotschen Verzerrungsellipsen, die in Abbildung 2 mit 15° Abstand voneinander bis 90° nördlicher und südlicher Breite und für 180° in Länge dargestellt sind. Die grossen Halbachsen a für φ=90° würden unendlich gross, während die kleinen b verschwinden.
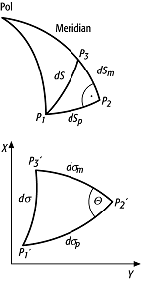 Flächenverzerrung 1: Berechnung der Flächenverzerrung. Flächenverzerrung 1: Berechnung der Flächenverzerrung.
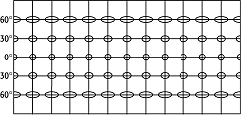 Flächenverzerrung 2: Tissotsche Verzerrungsellipsen der quadratischen Plattkarte. Flächenverzerrung 2: Tissotsche Verzerrungsellipsen der quadratischen Plattkarte. |
|