| |
der Unterschied der Grösse eines Winkel im Punkt P1 in der Bezugsfläche, der durch Grosskreisbögen P1P2 und P1P3 entsteht, und der Grösse des entsprechenden Winkels P2‘P1‘P3‘ in der Abbildungsebene. Wie aus der Verzerrungstheorie hervorgeht, muss im allgemeinen Fall, d.h. wenn dem Entwurf keine konforme Abbildung zugrunde liegt, in P1‘ die Winkelverzerrung vom Azimut abhängen, da die Längenverzerrung mα ebenfalls azimutabhängig ist. Es ist üblich, die Verzerrung des rechten Winkels zwischen Meridianen und Parallelkreisen in der Abbildungsebene mit

(Abb.) und die maximale Winkelverzerrung nach der Verzerrungstheorie mit 2Δω zu bezeichnen. Bei Kenntnis der Halbachsen a und b der Verzerrungsellipse ist nach der Verzerrungstheorie:
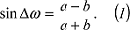 Dieser Ausdruck für die Winkelverzerrung kann mit den bekannten goniometrischen Zusammenhängen auch durch die anderen Winkelfunktionen ausgedrückt werden, nämlich: Dieser Ausdruck für die Winkelverzerrung kann mit den bekannten goniometrischen Zusammenhängen auch durch die anderen Winkelfunktionen ausgedrückt werden, nämlich:
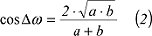 und: und:
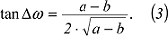 Wie schon erwähnt, sind die Achsen der Verzerrungsellipse a und b im allgemeinen nicht bekannt. Sie werden explizit nur benötigt, wenn man die Verzerrungen eines Kartennetzentwurfs durch Einzeichnen der Verzerrungsellipsen an vielen Punkten der Karte global charakterisieren will. Als zweckmässiger zur Berechnung der Winkelverzerrungen eines Entwurfs erweist sich die Verwendung der partiellen Differentiale fφ, fλ, gφ und gλ (Verzerrungstheorie Gleichung 14) und der Ausdrücke für die Längenverzerrung im Meridian mm und im Parallelkreis mp (Verzerrungstheorie Gleichung 19) sowie des Winkels Wie schon erwähnt, sind die Achsen der Verzerrungsellipse a und b im allgemeinen nicht bekannt. Sie werden explizit nur benötigt, wenn man die Verzerrungen eines Kartennetzentwurfs durch Einzeichnen der Verzerrungsellipsen an vielen Punkten der Karte global charakterisieren will. Als zweckmässiger zur Berechnung der Winkelverzerrungen eines Entwurfs erweist sich die Verwendung der partiellen Differentiale fφ, fλ, gφ und gλ (Verzerrungstheorie Gleichung 14) und der Ausdrücke für die Längenverzerrung im Meridian mm und im Parallelkreis mp (Verzerrungstheorie Gleichung 19) sowie des Winkels 
(Verzerrungstheorie Gleichung 41). Dazu sind die zwischen beiden Systemen bestehenden Zusammenhänge nachzuweisen.
In der Abbildung a) ist ein differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem
Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten
rechtwinkligen Koordinatensystem ξ,η. Der Parallelkreisbogen schliesst mit der η-Achse den gleichen
Winkel ω ein. Im Teil b der Abbildung ist X,Y das durch Affinität bestimmte Abbild des ξ-η-Systems. Das heisst, von M‘ aus liegt in der X-Richtung die grosse Achse der Verzerrungsellipse a und in der
Y-Richtung die kleine b.
Nach der Verzerrungstheorie (Gleichung 13) gilt die Längenverzerrung mα=mω in Richtung ω
bezogen auf die willkürlichen Ausgangsrichtungen ξ und η:
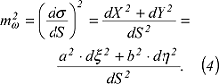 Der letzte Ausdruck gilt entsprechend der Gleichung 43 der Verzerrungstheorie wegen der in der Abbildung geltenden Affinität zwischen Kreis und Verzerrungsellipse. Aus der Abbildung liest man direkt ab für den Meridian: Der letzte Ausdruck gilt entsprechend der Gleichung 43 der Verzerrungstheorie wegen der in der Abbildung geltenden Affinität zwischen Kreis und Verzerrungsellipse. Aus der Abbildung liest man direkt ab für den Meridian:
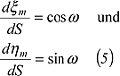 und für den Parallelkreis: und für den Parallelkreis:
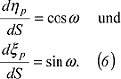 Durch Einsetzen von (5) und (6) in (4) findet man zwei Gleichungen: Durch Einsetzen von (5) und (6) in (4) findet man zwei Gleichungen:
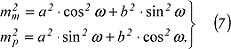 Die Summe der beiden Gleichungen (7) ergibt die gesuchte Beziehung zwischen den Halbachsen der Verzerrungsellipse a und b in der Ebene und den partiellen Differentialen fφ, fλ, gφ und gλ des sphärischen Differentialdreiecks: Die Summe der beiden Gleichungen (7) ergibt die gesuchte Beziehung zwischen den Halbachsen der Verzerrungsellipse a und b in der Ebene und den partiellen Differentialen fφ, fλ, gφ und gλ des sphärischen Differentialdreiecks:
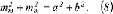 Gleichung (8) ist eine Gleichung mit zwei Unbekannten. Durch Hinzunahme einer weiteren Gleichung Gleichung (8) ist eine Gleichung mit zwei Unbekannten. Durch Hinzunahme einer weiteren Gleichung
aus der Flächenverzerrung:
vf=mm·mp·sin 
=a·b (9) wird die Umformung lösbar. Von Gleichung (3) ausgehend wird die Verbindung zwischen (8) und (9)
wie folgt geknüpft:
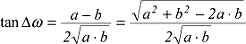 und schliesslich: und schliesslich:
 Mit Hilfe der Substitution: Mit Hilfe der Substitution:
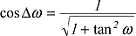 erhält man einen weiteren Ausdruck, nämlich: erhält man einen weiteren Ausdruck, nämlich:
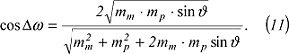 Schliesslich kann cosΔω in bekannter Weise in sinΔω umgewandelt werden: Schliesslich kann cosΔω in bekannter Weise in sinΔω umgewandelt werden:
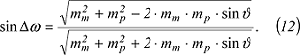 Die Gleichungen (10), (11) und (12) lassen sich durch Einführung der Flächenverzerrung vf nach Gleichung (9) vereinfachen. Eine wesentliche Vereinfachung ergibt sich für Entwürfe, bei denen die Bilder der Meridiane und der Parallele sich rechtwinklig schneiden, bei denen also Die Gleichungen (10), (11) und (12) lassen sich durch Einführung der Flächenverzerrung vf nach Gleichung (9) vereinfachen. Eine wesentliche Vereinfachung ergibt sich für Entwürfe, bei denen die Bilder der Meridiane und der Parallele sich rechtwinklig schneiden, bei denen also 
=90º gilt. Dann erhält man:
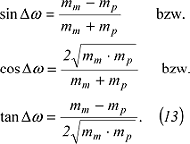 Literatur: [1] FIALA, F. (1957): Mathematische Kartographie. – Berlin. [2] WAGNER, K.H. (1949): Literatur: [1] FIALA, F. (1957): Mathematische Kartographie. – Berlin. [2] WAGNER, K.H. (1949):
Kartographische Netzentwürfe. - Leipzig.
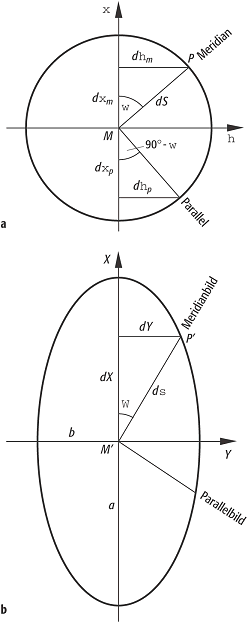 Winkelverzerrung: a) differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten rechtwinkligen Koordinatensystem ξ,η; b) X,Y ist das durch Affinität bestimmte Abbild des ξ-η-Systems.chied der Grösse eines Winkel im Punkt P1 in der Bezugsfläche, der durch Grosskreisbögen P1P2 und P1P3 entsteht, und der Grösse des entsprechenden Winkels P2‘P1‘P3‘ in der Abbildungsebene. Wie aus der Verzerrungstheorie hervorgeht, muss im allgemeinen Fall, d.h. wenn dem Entwurf keine konforme Abbildung zugrunde liegt, in P1‘ die Winkelverzerrung vom Azimut abhängen, da die Längenverzerrung mα ebenfalls azimutabhängig ist. Es ist üblich, die Verzerrung des rechten Winkels zwischen Meridianen und Parallelkreisen in der Abbildungsebene mit Winkelverzerrung: a) differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten rechtwinkligen Koordinatensystem ξ,η; b) X,Y ist das durch Affinität bestimmte Abbild des ξ-η-Systems.chied der Grösse eines Winkel im Punkt P1 in der Bezugsfläche, der durch Grosskreisbögen P1P2 und P1P3 entsteht, und der Grösse des entsprechenden Winkels P2‘P1‘P3‘ in der Abbildungsebene. Wie aus der Verzerrungstheorie hervorgeht, muss im allgemeinen Fall, d.h. wenn dem Entwurf keine konforme Abbildung zugrunde liegt, in P1‘ die Winkelverzerrung vom Azimut abhängen, da die Längenverzerrung mα ebenfalls azimutabhängig ist. Es ist üblich, die Verzerrung des rechten Winkels zwischen Meridianen und Parallelkreisen in der Abbildungsebene mit

(Abb.) und die maximale Winkelverzerrung nach der Verzerrungstheorie mit 2Δω zu bezeichnen. Bei Kenntnis der Halbachsen a und b der Verzerrungsellipse ist nach der Verzerrungstheorie:
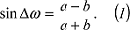 Dieser Ausdruck für die Winkelverzerrung kann mit den bekannten goniometrischen Zusammenhängen auch durch die anderen Winkelfunktionen ausgedrückt werden, nämlich: Dieser Ausdruck für die Winkelverzerrung kann mit den bekannten goniometrischen Zusammenhängen auch durch die anderen Winkelfunktionen ausgedrückt werden, nämlich:
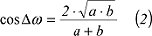 und: und:
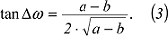 Wie schon erwähnt, sind die Achsen der Verzerrungsellipse a und b im allgemeinen nicht bekannt. Sie werden explizit nur benötigt, wenn man die Verzerrungen eines Kartennetzentwurfs durch Einzeichnen der Verzerrungsellipsen an vielen Punkten der Karte global charakterisieren will. Als zweckmässiger zur Berechnung der Winkelverzerrungen eines Entwurfs erweist sich die Verwendung der partiellen Differentiale fφ, fλ, gφ und gλ (Verzerrungstheorie Gleichung 14) und der Ausdrücke für die Längenverzerrung im Meridian mm und im Parallelkreis mp (Verzerrungstheorie Gleichung 19) sowie des Winkels Wie schon erwähnt, sind die Achsen der Verzerrungsellipse a und b im allgemeinen nicht bekannt. Sie werden explizit nur benötigt, wenn man die Verzerrungen eines Kartennetzentwurfs durch Einzeichnen der Verzerrungsellipsen an vielen Punkten der Karte global charakterisieren will. Als zweckmässiger zur Berechnung der Winkelverzerrungen eines Entwurfs erweist sich die Verwendung der partiellen Differentiale fφ, fλ, gφ und gλ (Verzerrungstheorie Gleichung 14) und der Ausdrücke für die Längenverzerrung im Meridian mm und im Parallelkreis mp (Verzerrungstheorie Gleichung 19) sowie des Winkels 
(Verzerrungstheorie Gleichung 41). Dazu sind die zwischen beiden Systemen bestehenden Zusammenhänge nachzuweisen.
In der Abbildung a) ist ein differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem
Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten
rechtwinkligen Koordinatensystem ξ,η. Der Parallelkreisbogen schliesst mit der η-Achse den gleichen
Winkel ω ein. Im Teil b der Abbildung ist X,Y das durch Affinität bestimmte Abbild des ξ-η-Systems. Das heisst, von M‘ aus liegt in der X-Richtung die grosse Achse der Verzerrungsellipse a und in der
Y-Richtung die kleine b.
Nach der Verzerrungstheorie (Gleichung 13) gilt die Längenverzerrung mα=mω in Richtung ω
bezogen auf die willkürlichen Ausgangsrichtungen ξ und η:
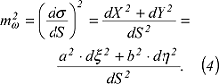 Der letzte Ausdruck gilt entsprechend der Gleichung 43 der Verzerrungstheorie wegen der in der Abbildung geltenden Affinität zwischen Kreis und Verzerrungsellipse. Aus der Abbildung liest man direkt ab für den Meridian: Der letzte Ausdruck gilt entsprechend der Gleichung 43 der Verzerrungstheorie wegen der in der Abbildung geltenden Affinität zwischen Kreis und Verzerrungsellipse. Aus der Abbildung liest man direkt ab für den Meridian:
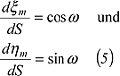 und für den Parallelkreis: und für den Parallelkreis:
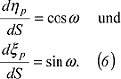 Durch Einsetzen von (5) und (6) in (4) findet man zwei Gleichungen: Durch Einsetzen von (5) und (6) in (4) findet man zwei Gleichungen:
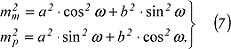 Die Summe der beiden Gleichungen (7) ergibt die gesuchte Beziehung zwischen den Halbachsen der Verzerrungsellipse a und b in der Ebene und den partiellen Differentialen fφ, fλ, gφ und gλ des sphärischen Differentialdreiecks: Die Summe der beiden Gleichungen (7) ergibt die gesuchte Beziehung zwischen den Halbachsen der Verzerrungsellipse a und b in der Ebene und den partiellen Differentialen fφ, fλ, gφ und gλ des sphärischen Differentialdreiecks:
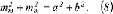 Gleichung (8) ist eine Gleichung mit zwei Unbekannten. Durch Hinzunahme einer weiteren Gleichung Gleichung (8) ist eine Gleichung mit zwei Unbekannten. Durch Hinzunahme einer weiteren Gleichung
aus der Flächenverzerrung:
vf=mm·mp·sin 
=a·b (9) wird die Umformung lösbar. Von Gleichung (3) ausgehend wird die Verbindung zwischen (8) und (9)
wie folgt geknüpft:
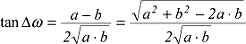 und schliesslich: und schliesslich:
 Mit Hilfe der Substitution: Mit Hilfe der Substitution:
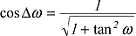 erhält man einen weiteren Ausdruck, nämlich: erhält man einen weiteren Ausdruck, nämlich:
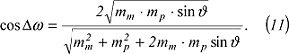 Schliesslich kann cosΔω in bekannter Weise in sinΔω umgewandelt werden: Schliesslich kann cosΔω in bekannter Weise in sinΔω umgewandelt werden:
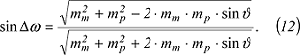 Die Gleichungen (10), (11) und (12) lassen sich durch Einführung der Flächenverzerrung vf nach Gleichung (9) vereinfachen. Eine wesentliche Vereinfachung ergibt sich für Entwürfe, bei denen die Bilder der Meridiane und der Parallele sich rechtwinklig schneiden, bei denen also Die Gleichungen (10), (11) und (12) lassen sich durch Einführung der Flächenverzerrung vf nach Gleichung (9) vereinfachen. Eine wesentliche Vereinfachung ergibt sich für Entwürfe, bei denen die Bilder der Meridiane und der Parallele sich rechtwinklig schneiden, bei denen also 
=90º gilt. Dann erhält man:
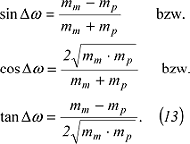 Literatur: [1] FIALA, F. (1957): Mathematische Kartographie. – Berlin. [2] WAGNER, K.H. (1949): Literatur: [1] FIALA, F. (1957): Mathematische Kartographie. – Berlin. [2] WAGNER, K.H. (1949):
Kartographische Netzentwürfe. - Leipzig.
 Winkelverzerrung: a) differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten rechtwinkligen Koordinatensystem ξ,η; b) X,Y ist das durch Affinität bestimmte Abbild des ξ-η-Systems. Winkelverzerrung: a) differentieller Kreis auf der Kugeloberfläche mit dem Radius dS und dem Winkel ω zwischen der Meridianrichtung MP und der ξ-Achse in einem beliebig um M orientierten rechtwinkligen Koordinatensystem ξ,η; b) X,Y ist das durch Affinität bestimmte Abbild des ξ-η-Systems. |
|