| |
dieses Brechungsgesetz beschreibt in Analogie zur Optik die Reflektions- und Brechungswinkel beim Einfall elastischer Wellen auf eine Fläche, die zwei Medien mit unterschiedlichen seismischen Geschwindigkeiten trennt. Mit einfachen strahlengeometrischen Überlegungen und dem Fermatschen Prinzip lässt es sich wie folgt ableiten (Abb.): eine ebene Welle, die von Punkt P im Medium mit der Geschwindigkeit V1 zum Punkt P‘ im Medium mit der Geschwindigkeit V2 läuft (es ist V1 < V2 angenommen). Der Weg von P nach P‘ ist durch den Wellenstrahl der Länge d im oberen und der Länge e im unteren Medium gegeben. Aufgabe ist es, Beziehungen für die Winkel i1 und i2 abzuleiten. Für die Laufzeit T zwischen P und P‘ gilt:
T=d/V1+e/V2=√{a2+x2}/V1+√{b2+(c-x)2}/V2.
Nach dem Fermatschen Prinzip erreicht die Laufzeit T ein Minimum, d.h. dT/dx=0. Damit ergibt sich:
x/{V1√a2+x2}-(c-x)/{V2√b2+(c-x)2}=0.
Wegen:
sin(i2)=(c-x)/√{b2+(c-x)2} und
sin(i1)=x/√{a2+x2} ergibt sich damit die aus der Optik bekannte Form des Snelliusschen Gesetzes: sin(i1)/V1=sin(i2)/V2.
Es gilt für reflektierte und gebrochene (refraktierte) Wellen und lässt sich auch auf Konversionen von P- nach S-Wellen und S- nach P-Wellen anwenden, die an der Trennfläche auftreten können. Die generalisierte Form des Snelliusschen Gesetzes ist p=sin(i)/V, wobei p als seismischer Parameter, Strahlparameter oder horizontale Slowness bezeichnet wird. Die Grösse p ist konstant entlang des gesamten Wellenstrahls. Daraus folgt, dass sich bei stetiger Änderung der Geschwindigkeit auch der Winkel i stetig ändert. Verläuft die Welle durch ein Gebiet mit zunehmender Geschwindigkeit, wird der Wellenstrahl fortgesetzt zur Horizontalen hin abgelenkt, bis er mit i=90º die Scheiteltiefe erreicht (Tauchwelle). Breitet sich die Welle hingegen durch ein Gebiet abnehmender Geschwindigkeit aus, wird der Wellenstrahl zur Vertikalen hin gebrochen. Kopfwellen entstehen an einer seismischen Diskontinuität erster Ordnung, wenn der Brechungswinkel i2 einen Wert von 90º erreicht. Dies ist nur möglich, wenn V1 < V2. Der dazugehörige Einfallswinkel i1 im oberen Medium wird als kritischer Winkel bezeichnet. Übersteigt der Einfallswinkel den Wert des kritischen Winkels, kann es zur Totalreflexion der einfallenden seismischen Welle kommen, vorausgesetzt, es wird keine Energie in das untere Medium durch Wechselwellen übertragen.
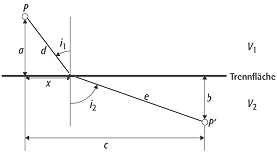 Snelliussches Brechungsgesetz: Wellenstrahlen zwischen den Punkten P und P‘, die in Medien mit unterschiedlichen seismischen Geschwindigkeiten liegen.Brechungsgesetz beschreibt in Analogie zur Optik die Reflektions- und Brechungswinkel beim Einfall elastischer Wellen auf eine Fläche, die zwei Medien mit unterschiedlichen seismischen Geschwindigkeiten trennt. Mit einfachen strahlengeometrischen Überlegungen und dem Fermatschen Prinzip lässt es sich wie folgt ableiten (Abb.): eine ebene Welle, die von Punkt P im Medium mit der Geschwindigkeit V1 zum Punkt P‘ im Medium mit der Geschwindigkeit V2 läuft (es ist V1 < V2 angenommen). Der Weg von P nach P‘ ist durch den Wellenstrahl der Länge d im oberen und der Länge e im unteren Medium gegeben. Aufgabe ist es, Beziehungen für die Winkel i1 und i2 abzuleiten. Für die Laufzeit T zwischen P und P‘ gilt: Snelliussches Brechungsgesetz: Wellenstrahlen zwischen den Punkten P und P‘, die in Medien mit unterschiedlichen seismischen Geschwindigkeiten liegen.Brechungsgesetz beschreibt in Analogie zur Optik die Reflektions- und Brechungswinkel beim Einfall elastischer Wellen auf eine Fläche, die zwei Medien mit unterschiedlichen seismischen Geschwindigkeiten trennt. Mit einfachen strahlengeometrischen Überlegungen und dem Fermatschen Prinzip lässt es sich wie folgt ableiten (Abb.): eine ebene Welle, die von Punkt P im Medium mit der Geschwindigkeit V1 zum Punkt P‘ im Medium mit der Geschwindigkeit V2 läuft (es ist V1 < V2 angenommen). Der Weg von P nach P‘ ist durch den Wellenstrahl der Länge d im oberen und der Länge e im unteren Medium gegeben. Aufgabe ist es, Beziehungen für die Winkel i1 und i2 abzuleiten. Für die Laufzeit T zwischen P und P‘ gilt:
T=d/V1+e/V2=√{a2+x2}/V1+√{b2+(c-x)2}/V2.
Nach dem Fermatschen Prinzip erreicht die Laufzeit T ein Minimum, d.h. dT/dx=0. Damit ergibt sich:
x/{V1√a2+x2}-(c-x)/{V2√b2+(c-x)2}=0.
Wegen:
sin(i2)=(c-x)/√{b2+(c-x)2} und
sin(i1)=x/√{a2+x2} ergibt sich damit die aus der Optik bekannte Form des Snelliusschen Gesetzes: sin(i1)/V1=sin(i2)/V2.
Es gilt für reflektierte und gebrochene (refraktierte) Wellen und lässt sich auch auf Konversionen von P- nach S-Wellen und S- nach P-Wellen anwenden, die an der Trennfläche auftreten können. Die generalisierte Form des Snelliusschen Gesetzes ist p=sin(i)/V, wobei p als seismischer Parameter, Strahlparameter oder horizontale Slowness bezeichnet wird. Die Grösse p ist konstant entlang des gesamten Wellenstrahls. Daraus folgt, dass sich bei stetiger Änderung der Geschwindigkeit auch der Winkel i stetig ändert. Verläuft die Welle durch ein Gebiet mit zunehmender Geschwindigkeit, wird der Wellenstrahl fortgesetzt zur Horizontalen hin abgelenkt, bis er mit i=90º die Scheiteltiefe erreicht (Tauchwelle). Breitet sich die Welle hingegen durch ein Gebiet abnehmender Geschwindigkeit aus, wird der Wellenstrahl zur Vertikalen hin gebrochen. Kopfwellen entstehen an einer seismischen Diskontinuität erster Ordnung, wenn der Brechungswinkel i2 einen Wert von 90º erreicht. Dies ist nur möglich, wenn V1 < V2. Der dazugehörige Einfallswinkel i1 im oberen Medium wird als kritischer Winkel bezeichnet. Übersteigt der Einfallswinkel den Wert des kritischen Winkels, kann es zur Totalreflexion der einfallenden seismischen Welle kommen, vorausgesetzt, es wird keine Energie in das untere Medium durch Wechselwellen übertragen.
 Snelliussches Brechungsgesetz: Wellenstrahlen zwischen den Punkten P und P‘, die in Medien mit unterschiedlichen seismischen Geschwindigkeiten liegen. Snelliussches Brechungsgesetz: Wellenstrahlen zwischen den Punkten P und P‘, die in Medien mit unterschiedlichen seismischen Geschwindigkeiten liegen. |
|