| |
Reduktionen, die zu den auf der Erdoberfläche gemessenen Schwerewerten addiert werden, um im Rahmen des Stokes-Problems die auf das Geoid bezogenen Schwereanomalien zu erhalten. Die Schwerereduktionen sind erforderlich, um die ausserhalb des Geoids liegenden topographischen Massen gedanklich zu beseitigen, so dass das Geoid Randfläche eines regularisierten Erdkörpers wird. Mit der topographischen Reduktion δgT wird der Einfluss der topographischen Massen auf die Schwere g im Aufpunkt P der Erdoberfläche beseitigt. δgT lässt sich nach dem Gravitationsgesetz berechnen. Dabei wird das Gelände entweder durch Kreisringe um den Aufpunkt und davon ausgehende Strahlen oder durch Quadrate in einem Koordinatengitter in vertikale Säulen zerlegt. Häufig wird die topographische Reduktion in die Bouguersche Plattenreduktion δgP und die Geländereduktion δgG aufgeteilt. Bei der Plattenreduktion wird die Gravitation einer unendlich ausgedehnten, horizontalen Platte (Bouguerplatte) konstanter Dichte ρ mit der Mächtigkeit der Aufpunktshöhe HP berücksichtigt (G=Gravitationskonstante, HP=orthometrische Höhe des Punktes P): δgP=2π·G·ρ·HP.
Mit dem Dichtewert ρ=2390 kg/m3 nimmt der Bouguer-Gradient den Wert 0,1·10-5s-2=0,1 mgal/m an. Die Geländereduktion δgG stellt gedanklich durch Abtragen der Massen oberhalb bzw. Auffüllen fehlender Massen unterhalb des Aufpunktniveaus eine horizontale Fläche her; δgG ist stets positiv.
Die isostatische Reduktion δgI resultiert aus der Verteilung der topographischen Massen unterhalb des Geoids nach einem Isostasiemodell. Auf diese Weise wird die Erdkruste gedanklich regularisiert, so dass eine Kruste konstanter Mächtigkeit und Dichte entsteht. Die isostatische Reduktion kann mittels einer Zerlegung der isostatischen Ausgleichsmassen in Kompartimente, die entweder von Kreisringen und Strahlen oder von Gitterlinien des Koordinatensystems begrenzt werden, und Summation über die Wirkungen aller Kompartimente berechnet werden. Mit der Freiluft-Reduktion δgF wird die gemessene, u.U. topographisch-isostatisch reduzierte Schwere auf das Geoid fortgesetzt. Wegen der Unkenntnis des Schwereverlaufs längs der Lotlinie wird im allgemeinen ein vereinfachtes Verfahren auf der Grundlage des Normalschweregradienten verwendet, der den tatsächlichen Schweregradienten ersetzt. Mit dem globalen Mittelwert des Freiluftgradienten ∂γ=∂η≈ -0,3086·10-5s-2=-0,3086 mgal/m ergibt sich die Rechenformel:
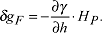 (HP=orthometrische Höhe des Aufpunktes P); nichtlineare Terme bezüglich HP werden i.a. nicht berücksichtigt. (HP=orthometrische Höhe des Aufpunktes P); nichtlineare Terme bezüglich HP werden i.a. nicht berücksichtigt. |
|