| |
in einem lokalen astronomischen System mit Ursprung im Punkt P auf der Äquipotentialfläche W(P)=const. (z-Achse zeigt in Lotrichtung zum Nadir, x- und y-Achse zeigen nach Norden bzw. Osten und spannen die lokale Tangentialebene in P auf) lässt sich der Schwerevektor (Schwere) als Gradient des Schwerepotentials darstellen:

=gradW. Durch nochmalige Gradientenbildung gelangt man auf den Tensor der zweiten (partiellen) Ableitungen des Schwerepotentials (Wij) (Eötvös-Tensor). Die letzte Zeile dieses Tensors gibt den Schweregradienten an (Wzx,Wzy,Wzz)=grad| 
|, wobei angenommen wird, dass | 
| ≈ Wz. Der horizontale Schweregradient in der lokalen Tangentialebene ist gegeben durch:
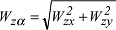 und zeigt in Richtung maximaler Schwereänderung, wobei sich mit α=arctanWzyWzx das Azimut ergibt. Der vertikale Schweregradient Wzz lässt sich unter Berücksichtigung der erweiterten Poisson-Gleichung schreiben als: und zeigt in Richtung maximaler Schwereänderung, wobei sich mit α=arctanWzyWzx das Azimut ergibt. Der vertikale Schweregradient Wzz lässt sich unter Berücksichtigung der erweiterten Poisson-Gleichung schreiben als:
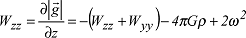 mit G=Gravitationskonstante, ρ=Dichte und ω=Winkelgeschwindigkeit der Erdrotation). In der Geodäsie und Geophysik ist der vertikale Schweregradient besonders wichtig für die Interpretation und Reduktion von Schweredaten. Der vertikale normale Schweregradient ∂γ/∂h wird aus dem Normalpotential als Approximation für den tatsächlichen vertikalen Schweregradienten erhalten. Ein gebräuchlicher Wert ist: mit G=Gravitationskonstante, ρ=Dichte und ω=Winkelgeschwindigkeit der Erdrotation). In der Geodäsie und Geophysik ist der vertikale Schweregradient besonders wichtig für die Interpretation und Reduktion von Schweredaten. Der vertikale normale Schweregradient ∂γ/∂h wird aus dem Normalpotential als Approximation für den tatsächlichen vertikalen Schweregradienten erhalten. Ein gebräuchlicher Wert ist:
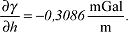 |
|