| |
Erdmodell, welches sowohl die Figur als auch das Schwerefeld der Erde global annähert. Nach dem Theorem von Stokes ist das Schwerepotential im Aussenraum einer gegebenen, um eine raumfeste Achse mit konstanter Winkelgeschwindigkeit ω rotierenden Fläche S eindeutig bestimmt, wenn das Schwerepotential auf S bekannt ist. Da ein an den Polen abgeplattetes Rotationsellipsoid mit der grossen Halbachse a und der kleinen Halbachse b die Figur der Erde bereits recht gut annähert, wird in der Regel ein solches Ellipsoid als geometrisches Erdmodell gewählt. Ferner wird vorausgesetzt, dass dieses Rotationsellipsoid um die kleine, polare Halbachse mit der konstanten Winkelgeschwindigkeit ω rotiert und das aus Gravitations- und Zentrifugaltermen zusammengesetzte Normalschwerepotential auf der Oberfläche des Rotationsellipsoids konstant ist. Ein mit diesen Eigenschaften ausgestattetes Rotationsellipsoid nennt man Niveauellipsoid. Über die das Normalschwerefeld im Aussenraum des Niveauellipsoids erzeugende innere Massenverteilung wird nichts ausgesagt. Nach der Theorie von Somigliana-Pizzetti gelingt eine geschlossene Darstellung des zugehörigen Normalschwerepotentials im System der elliptischen Koordinaten. Mit der linearen Exzentrizität:
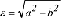 des Rotationsellipsoids gilt zwischen den elliptischen Koordinaten u,β,λ und den kartesischen Koordinaten x,y,z des des Rotationsellipsoids gilt zwischen den elliptischen Koordinaten u,β,λ und den kartesischen Koordinaten x,y,z des 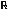
3 die folgende Beziehung:
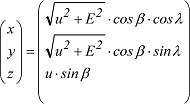 mit u=kleine Halbachse, β =reduzierte Breite und λ = geographische Länge. Für das Normalschwerepotential U im Aussenraum gilt die Darstellung: mit u=kleine Halbachse, β =reduzierte Breite und λ = geographische Länge. Für das Normalschwerepotential U im Aussenraum gilt die Darstellung:
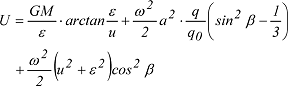 mit den Hilfsgrössen q und q0: mit den Hilfsgrössen q und q0:
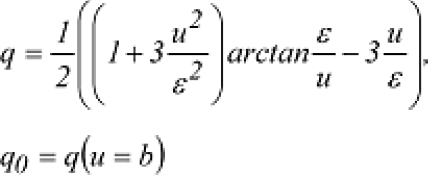 und der geozentrischen Gravitationskonstanten GM. Das auf der Ellipsoidoberfläche konstante Normalschwerepotential U=U0 besitzt den Potentialwert: und der geozentrischen Gravitationskonstanten GM. Das auf der Ellipsoidoberfläche konstante Normalschwerepotential U=U0 besitzt den Potentialwert:
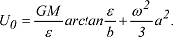 Durch Festlegung der vier Parameter a,b,U0,ω ist das Normalpotential eindeutig festgelegt; anstelle dieses Parametersatzes kann auch das Quadrupel a,J2,GM,ω benutzt werden, wobei J2=-C20 der zonale Kugelfunktionskoeffizient zweiten Grades ist. Numerische Werte dieser vier Fundamentalparameter sind von der Internationalen Assoziation für Geodäsie offiziell in den geodätischen Referenzsystemen, zuletzt GRS80, festgelegt worden. Durch Ableitung des Normalpotentials U entsteht der Normalschwerevektor Durch Festlegung der vier Parameter a,b,U0,ω ist das Normalpotential eindeutig festgelegt; anstelle dieses Parametersatzes kann auch das Quadrupel a,J2,GM,ω benutzt werden, wobei J2=-C20 der zonale Kugelfunktionskoeffizient zweiten Grades ist. Numerische Werte dieser vier Fundamentalparameter sind von der Internationalen Assoziation für Geodäsie offiziell in den geodätischen Referenzsystemen, zuletzt GRS80, festgelegt worden. Durch Ableitung des Normalpotentials U entsteht der Normalschwerevektor
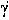
= grad U, dessen Betrag als Normalschwere bezeichnet wird. Der Normalschwerevektor 
steht in jedem Punkt P senkrecht auf der durch P laufenden Äquipotentialfläche U =U(P)=const. Eine solche, durch einen beliebigen Punkt P verlaufende Äquipotentialfläche des Normalschwerefeldes wird auch als Sphärop bezeichnet; mit Ausnahme der Randfläche des Niveauellipsoids sind diese Äquipotentialflächen keine Ellipsoide. Aus der Theorie von Somigliana und Pizzetti folgt das Theorem von Clairaut:
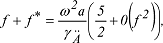 welches die geometrische Abplattung f=(a-b)/a mit der gravimetrischen Abplattung: welches die geometrische Abplattung f=(a-b)/a mit der gravimetrischen Abplattung:
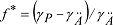 verbindet, mit γÄ,γP Normalschwere am Äquator bzw. an den Polen. Da die elliptischen Koordinaten u,β,λ wenig anschaulich sind, geht man gewöhnlich auf die in der Praxis häufig verwendeten Polarkoordinaten λ,r=geozentrischer Abstand und ψ = geozentrische Breite über, wodurch die geschlossene Darstellung des Normalpotentials U in eine unendliche Reihe der Form: verbindet, mit γÄ,γP Normalschwere am Äquator bzw. an den Polen. Da die elliptischen Koordinaten u,β,λ wenig anschaulich sind, geht man gewöhnlich auf die in der Praxis häufig verwendeten Polarkoordinaten λ,r=geozentrischer Abstand und ψ = geozentrische Breite über, wodurch die geschlossene Darstellung des Normalpotentials U in eine unendliche Reihe der Form:
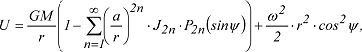 mit P2n(sinψ)=Legendresche Polynome geraden Grades, übergeht. Alle Kugelfunktionskoeffizienten J2n mit n > 1 können als Funktion der ersten numerischen Exzentrizität e des Ellipsoids und des Kugelfunktionskoeffizienten zweiten Grades J2 dargestellt werden: mit P2n(sinψ)=Legendresche Polynome geraden Grades, übergeht. Alle Kugelfunktionskoeffizienten J2n mit n > 1 können als Funktion der ersten numerischen Exzentrizität e des Ellipsoids und des Kugelfunktionskoeffizienten zweiten Grades J2 dargestellt werden:
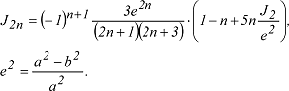 Diese Reihe konvergiert sehr rasch, so dass in der Regel eine Summation bis n=4 ausreicht. Diese Reihe konvergiert sehr rasch, so dass in der Regel eine Summation bis n=4 ausreicht. |
|