| |
Newtonsches Raumpotential, Bezeichnung für das Potential V, der aus dem Newtonschen Gravitationsgesetz (Gravitation) folgenden konservativen Gravitationsfeldstärke eines anziehenden Massenpunktes. Für ausgedehnte (nicht notwendigerweise sphärisch-homogene) Körper (und damit für die Erde) lässt sich die Quellendarstellung des Gravitationspotentials in einem dreidimensionalen, kartesischen Koordinatensystem angeben:
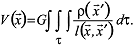 Dabei ist τ das geschlossene, beschränkte Raumgebiet (Volumen des betrachteten Körpers), P( Dabei ist τ das geschlossene, beschränkte Raumgebiet (Volumen des betrachteten Körpers), P(
) der Aufpunkt (der bei der Berechnung feste Punkt), Q( 
') der Quellpunkt (der unter der Integration laufende Punkt), ρ( 
') die auf τ beschränkte Dichteverteilung, l( 
, 
')=| 
-
'| der Abstand zwischen Auf- und Quellpunkt und ρ( 
')dτ = dm das differentielle Massenelement (die Massenbelegung). Die Funktion 1/l( 
, 
') wird als Newtonscher Kern bezeichnet und spielt eine herausragende Rolle in der Potentialtheorie. Das Gravitationspotential ist im Aussenraum einschliesslich seiner ersten und zweiten partiellen Ableitungen endlich und stetig. V ist regulär im Unendlichen:
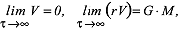 wobei M die Gesamtmasse auf τ (z.B. die Erde) ist. Physikalisch ist damit das Gravitationspotential äquivalent der potentiellen Energie, deren Nullreferenzniveau ins Unendliche verlegt ist. Da die Dichteverteilung im Aussenraum von τ verschwindet, bildet der Gravitationsvektor gradV ein quellenfreies Vektorfeld, es gilt damit im Aussenraum die Laplace-Gleichung ΔV = 0. Im Innenraum erfüllt V die Poisson-Gleichung ΔV =-4πGρ. Das Gravitationspotential kann im Aussenraum durch Lösen eines geodätischen Randwertproblems bestimmt werden, im Innenraum nur bei bekannter Dichteverteilung ρ( wobei M die Gesamtmasse auf τ (z.B. die Erde) ist. Physikalisch ist damit das Gravitationspotential äquivalent der potentiellen Energie, deren Nullreferenzniveau ins Unendliche verlegt ist. Da die Dichteverteilung im Aussenraum von τ verschwindet, bildet der Gravitationsvektor gradV ein quellenfreies Vektorfeld, es gilt damit im Aussenraum die Laplace-Gleichung ΔV = 0. Im Innenraum erfüllt V die Poisson-Gleichung ΔV =-4πGρ. Das Gravitationspotential kann im Aussenraum durch Lösen eines geodätischen Randwertproblems bestimmt werden, im Innenraum nur bei bekannter Dichteverteilung ρ( 
'). Eine bevorzugte Methode zur Bestimmung des Gravitationspotentials im Aussenraum ist die Kugelfunktionsentwicklung des Gravitationspotentials. Die Quellendarstellung der Potentialkoeffizienten des Gravitationspotentials ist durch Volumenintegrale über die Erde möglich. Die differentialgeometrischen Eigenschaften des Gravitationspotentials können mit Hilfe des Eötvös-Tensors beschrieben werden. Dazu wird dieser in einem lokalen Tangentialsystem wie folgt geschrieben (Ursprung im Punkt P der Äquipotentialfläche V(P)= const. des Gravitationspotentials V, lokale z-Achse als Normale der Äquipotentialfläche entgegengesetzt zur Richtung des Gravitationsvektors 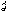
= gradV, lokale x-Achse (Nordrichtung) und lokale y-Achse (Westrichtung) spannen die Tangentialebene an die Äquipotentialfläche in P auf):
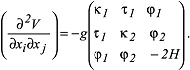 Dabei sind κ1 bzw. κ2 die Krümmung der Äquipotentialfläche V(P)=const. in Nord-Süd- bzw. West-Ost-Richtung, τ1 die Torsion des Meridians sowie φ1 bzw. φ2 die Krümmung der durch P verlaufenden Lotlinie in Nord-Süd- bzw. West-Ost-Richtung. Die mittlere Krümmung wird durch H und die Gausssche Krümmung durch K = κ1 ·κ2 beschrieben. MSc Dabei sind κ1 bzw. κ2 die Krümmung der Äquipotentialfläche V(P)=const. in Nord-Süd- bzw. West-Ost-Richtung, τ1 die Torsion des Meridians sowie φ1 bzw. φ2 die Krümmung der durch P verlaufenden Lotlinie in Nord-Süd- bzw. West-Ost-Richtung. Die mittlere Krümmung wird durch H und die Gausssche Krümmung durch K = κ1 ·κ2 beschrieben. MSc |
|