| |
die für eine skalare Feldfunktion u definierte inhomogene, partielle Differentialgleichung 2. Ordnung Δu=f (inhomogene Potentialgleichung). Mit dem Laplace-Operator Δ lässt sich die Poisson-Gleichung in einem dreidimensionalen, kartesischen Koordinatensystem schreiben als:
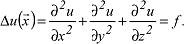 Eine koordinatenfreie Darstellung findet man mit Hilfe des Nablaoperators ∇: Eine koordinatenfreie Darstellung findet man mit Hilfe des Nablaoperators ∇:
Δu=∇2u=divgradu.
Die Poisson-Gleichung gehört zur Klasse der elliptischen Differentialgleichungen, die in den partiellen Ableitungen zweiter Ordnung linear sind und eine grosse Anzahl stationärer Prozesse beschreiben.
Sie ist deshalb von grosser Bedeutung bei der Beschreibung des Gravitationspotentials V. V genügt
innerhalb anziehender Massen, die durch eine Dichteverteilung darstellbar sind, der
Poisson-Gleichung, wobei die rechte Seite f proportional zu dieser Massendichte ρ ist: f=-4πGρ. Für
f=0 ergibt sich die homogene Potentialgleichung, die Laplace-Gleichung. |
|