| |
isotherme Flächenkoordinaten, konforme Koordinaten, Flächenkoordinaten (u,v) auf der Oberfläche einer Kugel oder eines Rotationsellipsoids, für die das Bogenelement die isotherme Form:
ds2 = λ2(u,v)·(du2+dv2) mit dem von den Parametern u,v abhängigen Faktor λ2(u,v) annimmt. Ein aus Gaussschen Koordinaten gebildetes isothermes Parameternetz zerlegt, wenn man die Koordinatendifferentiale du,dv gleichsetzt, die Fläche in infinitesimale Quadrate mit der Seitenlänge:
ds1 = ds2 = λ(u,v)·du = λ(u,v)·dv
und ist somit orthogonal. Kleinräumig können Gausssche Koordinaten deshalb wie geradlinige, ebene orthogonale Koordinaten (zweidimensionale kartesische Koordinaten) behandelt werden. Wichtige Spezialfälle Gaussscher Koordinaten sind die Gauss-Krüger-Koordinaten und die UTM-Koordinaten.
Werden auf derselben Fläche zwei verschiedene Systeme Gaussscher Koordinaten (u,v) und (
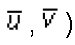 eingeführt, so gelten für die Transformationsbeziehungen:
u = f(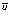 
, 
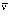
), v = g(
,
) die Cauchy-Riemannschen Differentialgleichungen:
 entsprechende Beziehungen gelten auch für die Umkehrtransformation. Aufgrund dieser Eigenschaft können f und g als Real- und Imaginärteile einer analytischen Funktion der komplexen Veränderlichen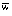 
= 
+i
mit i = √-1 aufgefasst werden:
w = u+iv = f( 
, 
)+i·g( 
, 
)= F(
+i 
)= F( 
).
Jede Transformation zwischen zwei Systemen Gaussscher isothermer Flächenkoordinaten auf einer
reellen analytischen Fläche kann deshalb durch eine analytische Funktion F dargestellt werden.
Umgekehrt können aus einem vorgegebenen isothermen Parametersystem sämtliche anderen
isothermen Parametersysteme der Fläche mit Hilfe analytischer Funktionen gewonnen werden. Neben der Interpretation von Gaussschen Koordinaten als Flächenparameter können diese formal
auch als ebene kartesische Koordinaten gedeutet werden, die aus einer Abbildung der Fläche auf die
Ebene entstanden sind. Identifiziert man die Zahlenwerte der Gaussschen Koordinaten ( 
, 
)mit den
kartesischen Koordinaten (X,Y) der euklidischen Ebene X =
, Y = 
, so wird durch diese isothermen
Parameter eine konforme Abbildung der Fläche auf die Ebene vermittelt. Aus diesen Gründen werden
Gausssche Koordinaten (z.B. Gauss-Krüger- oder UTM-Koordinaten) oft wie ebene kartesische
Koordinaten behandelt. Handelt es sich jedoch wie bei Kugel- und Ellipsoidflächen um Flächen, die
nicht in die Ebene abwickelbar sind, so entstehen durch die konforme Abbildung Verzerrungen, die in
Form von Reduktionen (Streckenreduktion, Richtungsreduktion) berücksichtigt werden.
BH
 |
|
