| |
1) beschreibt die Ausbreitung von Wellen als Funktion von Ort und Zeit. Fû¥r
eine in x-Richtung laufende Welle u gilt: u=Asin(kx-üt+ö).
Hierbei ist A die Amplitude, k die Wellenzahl, x die Ortskoordinate, ü die Kreisfrequenz, t die Zeit und
ö der Phasenwinkel. Fû¥r die Periode T, Frequenz f und WellenlûÊnge ö£ gelten: T=1/f=2ü/ü,
ö£=2ü/k.
Die durch konstante Werte von kx-üt definierten Punkte haben die gleichen Werte fû¥r u, sie bilden die Wellenfront. Sie breiten sich in x-Richtung mit der Phasengeschwindigkeit:
v=ü/k=ö£/T
aus. Durch Einfû¥hren von v in obige Gleichung und nach zweimaligem Differenzieren nach x und t
erhûÊlt man die eindimensionale Wellengleichung: 2ã2u/ãt2=v2ã2u/ãx. Sie lûÊsst sich leicht auf die Ausbreitung ebener Wellen (d.h. die Wellenfronten sind ebene FlûÊchen) im dreidimensionalen x,y,z-Koordinatensystem erweitern. Ersetzen muss man den Term kx durch das Skalarprodukt von Wellenzahlvektor 
=(kx,ky,kz) mit dem Ortsvektor 
=(x,y,z) und den eindimensionalen Operator ã2/ãx2 durch ã2/ãx2+ã2/ãy2+ã2/ãz2. Der Wellenzahlvektor zeigt in Ausbreitungsrichtung der ebenen Welle. Durch Superposition von ebenen Wellen lassen sich Kugelwellen berechnen. ûhnliche Wellengleichungen gelten fû¥r die Ausbreitung von P- und S-Wellen durch elastische, homogene und isotrope KûÑrper (Kontinuumsmechanik). Dabei wird u bei P-Wellen durch ein Skalarpotential ü und fû¥r S-Wellen durch ein Vektorpotential ö´ ersetzt. Aus den Potentialen lassen sich die Partikelverschiebungen berechnen. Die Geschwindigkeit v steht dann fû¥r die P- und S-Wellengeschwindigkeit im elastischen Medium.
2) Beziehung fû¥r das raum-zeitliche Verhalten von physikalischen FeldgrûÑssen. In der Elektrodynamik folgt z.B. aus den Maxwellschen Gleichungen die Telegraphengleichung fû¥r die elektrische FeldstûÊrke 
oder die Induktionsflussdichte 
(zusammenfassend mit 
bezeichnet):
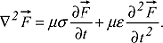 Dabei ist ö¥ die PermeabilitûÊt, ö die PermittivitûÊt und ü die elektrische LeitfûÊhigkeit. Der 1. Term der Gleichung kennzeichnet eine Diffusion des Feldes, der 2. eine Wellenausbreitung. Das relative Gewicht der beiden Terme wird durch den Verlustwinkel ö¡ beschrieben: Dabei ist ö¥ die PermeabilitûÊt, ö die PermittivitûÊt und ü die elektrische LeitfûÊhigkeit. Der 1. Term der Gleichung kennzeichnet eine Diffusion des Feldes, der 2. eine Wellenausbreitung. Das relative Gewicht der beiden Terme wird durch den Verlustwinkel ö¡ beschrieben:
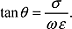 ibt die Ausbreitung von Wellen als Funktion von Ort und Zeit. Fû¥r ibt die Ausbreitung von Wellen als Funktion von Ort und Zeit. Fû¥r
eine in x-Richtung laufende Welle u gilt: u=Asin(kx-üt+ö).
Hierbei ist A die Amplitude, k die Wellenzahl, x die Ortskoordinate, ü die Kreisfrequenz, t die Zeit und
ö der Phasenwinkel. Fû¥r die Periode T, Frequenz f und WellenlûÊnge ö£ gelten: T=1/f=2ü/ü,
ö£=2ü/k.
Die durch konstante Werte von kx-üt definierten Punkte haben die gleichen Werte fû¥r u, sie bilden die Wellenfront. Sie breiten sich in x-Richtung mit der Phasengeschwindigkeit:
v=ü/k=ö£/T
aus. Durch Einfû¥hren von v in obige Gleichung und nach zweimaligem Differenzieren nach x und t
erhûÊlt man die eindimensionale Wellengleichung: 2ã2u/ãt2=v2ã2u/ãx. Sie lûÊsst sich leicht auf die Ausbreitung ebener Wellen (d.h. die Wellenfronten sind ebene FlûÊchen) im dreidimensionalen x,y,z-Koordinatensystem erweitern. Ersetzen muss man den Term kx durch das Skalarprodukt von Wellenzahlvektor 
=(kx,ky,kz) mit dem Ortsvektor 
=(x,y,z) und den eindimensionalen Operator ã2/ãx2 durch ã2/ãx2+ã2/ãy2+ã2/ãz2. Der Wellenzahlvektor zeigt in Ausbreitungsrichtung der ebenen Welle. Durch Superposition von ebenen Wellen lassen sich Kugelwellen berechnen. ûhnliche Wellengleichungen gelten fû¥r die Ausbreitung von P- und S-Wellen durch elastische, homogene und isotrope KûÑrper (Kontinuumsmechanik). Dabei wird u bei P-Wellen durch ein Skalarpotential ü und fû¥r S-Wellen durch ein Vektorpotential ö´ ersetzt. Aus den Potentialen lassen sich die Partikelverschiebungen berechnen. Die Geschwindigkeit v steht dann fû¥r die P- und S-Wellengeschwindigkeit im elastischen Medium.
2) Beziehung fû¥r das raum-zeitliche Verhalten von physikalischen FeldgrûÑssen. In der Elektrodynamik folgt z.B. aus den Maxwellschen Gleichungen die Telegraphengleichung fû¥r die elektrische FeldstûÊrke 
oder die Induktionsflussdichte 
(zusammenfassend mit 
bezeichnet):
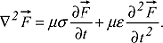 Dabei ist ö¥ die PermeabilitûÊt, ö die PermittivitûÊt und ü die elektrische LeitfûÊhigkeit. Der 1. Term der Gleichung kennzeichnet eine Diffusion des Feldes, der 2. eine Wellenausbreitung. Das relative Gewicht der beiden Terme wird durch den Verlustwinkel ö¡ beschrieben: Dabei ist ö¥ die PermeabilitûÊt, ö die PermittivitûÊt und ü die elektrische LeitfûÊhigkeit. Der 1. Term der Gleichung kennzeichnet eine Diffusion des Feldes, der 2. eine Wellenausbreitung. Das relative Gewicht der beiden Terme wird durch den Verlustwinkel ö¡ beschrieben:
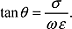 |
|