| |
Randwertproblem auf der Basis der folgenden Annahme: Sei τ ein geschlossenes, beschränktes Gebiet des dreidimensionalen Raumes mit Massenbelegung, τ* der Aussenraum von τ und σ die Randfläche von τ sowie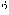 
der stetige Einheitsvektor der nach aussen gerichteten Normalen von τ. Existiert die harmonische Funktion (Potentialtheorie) u( 
), die im Aussenraum τ* der Laplace-Gleichung genüge und in τ* einschliesslich ihrer ersten und zweiten Ableitungen stetig sowie mit:
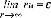 beschränkt ist, so lassen sich spezielle Lösungen u( 
) der Laplace-Gleichung finden, indem auf dem Rand des σ die Massenbelegung einschliessenden Raumgebietes τ zusätzliche Bedingungen, die Randbedingungen, eingeführt werden. Die Formulierung der Laplace-Gleichung zusammen mit Randbedingungen führt auf ein Randwertproblem der Potentialtheorie. Folgende Randwertprobleme lassen sich unterscheiden: Randwertproblem (Dirichlet-Problem): Gesucht ist eine im Aussenraum τ* des geschlossenen Raumgebietes τ einschliesslich seiner Randfläche σ stetige Funktion u( 
) mit Δu=0 in τ* sowie u=f( 
) auf σ. f( 
) ist eine auf σ gegebene, stetige Funktion. Randwertproblem (Neumann-Problem): Gesucht ist eine im Aussenraum τ* des geschlossenen Raumgebietes τ einschliesslich seiner Randfläche σ stetige Funktion u( 
) mit Δu=0 in τ* sowie auf σ. g( 
) ist eine auf σ gegebene, stetige Funktion.
Randwertproblem (gemischtes oder ROBIN-Problem): Gesucht ist eine im Aussenraum τ* des geschlossenen Raumgebietes τ einschliesslich seiner Randfläche σ stetige Funktion u( 
) mit Δu=0 in τ* sowie
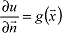
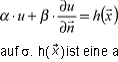
)ist eine auf σ aufgegebene, stetige Funktion. |
|
