|
| |
|
| |
Laplacesche Kugelflächenfunktionen |
|
| |
|
|
| |
Darstellung des Gravitationspotentials der Erde durch eine Reihenentwicklung nach Kugelflächenfunktionen. Sie beruht auf der Lösung der Laplaceschen Differentialgleichung ΔV= 0 für das Potential V. Bei der Herleitung der Lösung wird zunächst die Laplacesche Differentialgleichung unter Verwendung von Kugelkoordinaten umgeschrieben, so dass sich die Abhängigkeiten der Gleichungsterme in Abhängigkeiten nach r, nach θ und nach λ separieren lassen. Es ergibt sich, dass sich die Lösungen als allgemeinste ganze rationale räumliche Kugelfunktionen n-ten Grades in der Form:
Un =rnSn(θ,λ) darstellen lässt, wobei Un ein Polynom n-ten Grades in x, y, z ist, das von höchstens 2n+1 Konstanten linear-homogen abhängt. Sn(θ,λ) wird Laplacesche Kugelfunktion n-ten Grades genannt. Sie genügt, nachdem die Abhängigkeit nach r aus der Laplaceschen Differentialgleichung separiert worden war,
der Differentialgleichung:
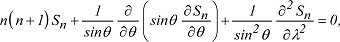 die linear homogen ist. Man erhält eine Lösung: die linear homogen ist. Man erhält eine Lösung:
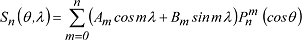 mit 2n+1 Konstanten A0, A1,..., An, B0, B1,..., Bn. Dabei sind die Pnm(cosθ) die zugeordneten Kugelfunktionen (Legendre-Funktionen 1. Art). Diese Lösung ist die allgemeinste Laplacesche Kugelfunktion (Kugelflächenfunktion) weil sie, mit rn multipliziert, ein homogenes Polynom n-ten Grades in x, y, z ist und die 2n+1 Glieder, aus denen sie linear homogen zusammengesetzt ist, linear unabhängig sind. Es ergeben sich die Laplaceschen Kugelflächenfunktionen der Grade zwei bis acht (Abb.). Laplacesche Kugelflächenfunktionen des Grades n setzen sich aus der Linearkombination von 2n+1 Kugelflächenfunktionen des Grades n und der Ordnungen m für m = 0,...,n zusammen: mit 2n+1 Konstanten A0, A1,..., An, B0, B1,..., Bn. Dabei sind die Pnm(cosθ) die zugeordneten Kugelfunktionen (Legendre-Funktionen 1. Art). Diese Lösung ist die allgemeinste Laplacesche Kugelfunktion (Kugelflächenfunktion) weil sie, mit rn multipliziert, ein homogenes Polynom n-ten Grades in x, y, z ist und die 2n+1 Glieder, aus denen sie linear homogen zusammengesetzt ist, linear unabhängig sind. Es ergeben sich die Laplaceschen Kugelflächenfunktionen der Grade zwei bis acht (Abb.). Laplacesche Kugelflächenfunktionen des Grades n setzen sich aus der Linearkombination von 2n+1 Kugelflächenfunktionen des Grades n und der Ordnungen m für m = 0,...,n zusammen:
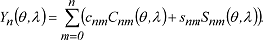 Sie bilden ein orthogonales Funktionensystem auf der Einheitskugel mit den Orthogonalitätsrelationen (δnm'= Kronecker-Symbol): Sie bilden ein orthogonales Funktionensystem auf der Einheitskugel mit den Orthogonalitätsrelationen (δnm'= Kronecker-Symbol):
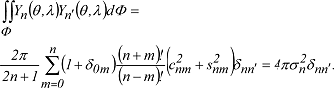 2Die Normen der Laplaceschen Kugelflächenfunktionen enthalten die Konstanten cnm , snm2 bzw. die Gradvarianzen σn2. 2Die Normen der Laplaceschen Kugelflächenfunktionen enthalten die Konstanten cnm , snm2 bzw. die Gradvarianzen σn2.
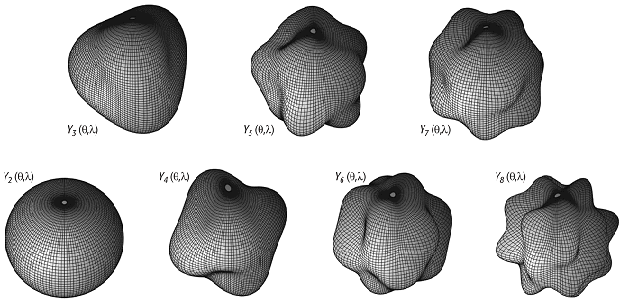 Laplacesche Kugelflächenfunktionen: Laplacesche Kugelflächenfunktionen der Grade zwei bis acht (überhöhte Funktionswerte unterschiedlichen Massstabes).g des Gravitationspotentials der Erde durch eine Reihenentwicklung nach Kugelflächenfunktionen. Sie beruht auf der Lösung der Laplaceschen Differentialgleichung ΔV= 0 für das Potential V. Bei der Herleitung der Lösung wird zunächst die Laplacesche Differentialgleichung unter Verwendung von Kugelkoordinaten umgeschrieben, so dass sich die Abhängigkeiten der Gleichungsterme in Abhängigkeiten nach r, nach θ und nach λ separieren lassen. Es ergibt sich, dass sich die Lösungen als allgemeinste ganze rationale räumliche Kugelfunktionen n-ten Grades in der Form: Laplacesche Kugelflächenfunktionen: Laplacesche Kugelflächenfunktionen der Grade zwei bis acht (überhöhte Funktionswerte unterschiedlichen Massstabes).g des Gravitationspotentials der Erde durch eine Reihenentwicklung nach Kugelflächenfunktionen. Sie beruht auf der Lösung der Laplaceschen Differentialgleichung ΔV= 0 für das Potential V. Bei der Herleitung der Lösung wird zunächst die Laplacesche Differentialgleichung unter Verwendung von Kugelkoordinaten umgeschrieben, so dass sich die Abhängigkeiten der Gleichungsterme in Abhängigkeiten nach r, nach θ und nach λ separieren lassen. Es ergibt sich, dass sich die Lösungen als allgemeinste ganze rationale räumliche Kugelfunktionen n-ten Grades in der Form:
Un =rnSn(θ,λ) darstellen lässt, wobei Un ein Polynom n-ten Grades in x, y, z ist, das von höchstens 2n+1 Konstanten linear-homogen abhängt. Sn(θ,λ) wird Laplacesche Kugelfunktion n-ten Grades genannt. Sie genügt, nachdem die Abhängigkeit nach r aus der Laplaceschen Differentialgleichung separiert worden war,
der Differentialgleichung:
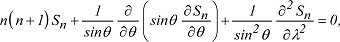 die linear homogen ist. Man erhält eine Lösung: die linear homogen ist. Man erhält eine Lösung:
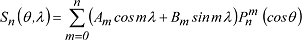 mit 2n+1 Konstanten A0, A1,..., An, B0, B1,..., Bn. Dabei sind die Pnm(cosθ) die zugeordneten Kugelfunktionen (Legendre-Funktionen 1. Art). Diese Lösung ist die allgemeinste Laplacesche Kugelfunktion (Kugelflächenfunktion) weil sie, mit rn multipliziert, ein homogenes Polynom n-ten Grades in x, y, z ist und die 2n+1 Glieder, aus denen sie linear homogen zusammengesetzt ist, linear unabhängig sind. Es ergeben sich die Laplaceschen Kugelflächenfunktionen der Grade zwei bis acht (Abb.). Laplacesche Kugelflächenfunktionen des Grades n setzen sich aus der Linearkombination von 2n+1 Kugelflächenfunktionen des Grades n und der Ordnungen m für m = 0,...,n zusammen: mit 2n+1 Konstanten A0, A1,..., An, B0, B1,..., Bn. Dabei sind die Pnm(cosθ) die zugeordneten Kugelfunktionen (Legendre-Funktionen 1. Art). Diese Lösung ist die allgemeinste Laplacesche Kugelfunktion (Kugelflächenfunktion) weil sie, mit rn multipliziert, ein homogenes Polynom n-ten Grades in x, y, z ist und die 2n+1 Glieder, aus denen sie linear homogen zusammengesetzt ist, linear unabhängig sind. Es ergeben sich die Laplaceschen Kugelflächenfunktionen der Grade zwei bis acht (Abb.). Laplacesche Kugelflächenfunktionen des Grades n setzen sich aus der Linearkombination von 2n+1 Kugelflächenfunktionen des Grades n und der Ordnungen m für m = 0,...,n zusammen:
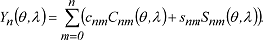 Sie bilden ein orthogonales Funktionensystem auf der Einheitskugel mit den Orthogonalitätsrelationen (δnm'= Kronecker-Symbol): Sie bilden ein orthogonales Funktionensystem auf der Einheitskugel mit den Orthogonalitätsrelationen (δnm'= Kronecker-Symbol):
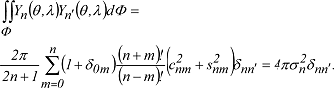 2Die Normen der Laplaceschen Kugelflächenfunktionen enthalten die Konstanten cnm , snm2 bzw. die Gradvarianzen σn2. 2Die Normen der Laplaceschen Kugelflächenfunktionen enthalten die Konstanten cnm , snm2 bzw. die Gradvarianzen σn2.
 Laplacesche Kugelflächenfunktionen: Laplacesche Kugelflächenfunktionen der Grade zwei bis acht (überhöhte Funktionswerte unterschiedlichen Massstabes). Laplacesche Kugelflächenfunktionen: Laplacesche Kugelflächenfunktionen der Grade zwei bis acht (überhöhte Funktionswerte unterschiedlichen Massstabes). |
|
| |
|
|
| |
Ein Bookmark auf diese Seite setzen:
|
|
| |
|
|
| |
<< vorheriger Begriff |
|
nächster Begriff >> |
|
|
|
|
|
| |
|
|
|
|