| |
Funktionen Pnm (t) (Legendresche Polynome 1. Art), die man fû¥r viele Reihenentwicklungen in der Geophysik wie im Geomagnetismus und in der Gravimetrie verwendet, wenn z.B. LûÑsungen der Laplace- bzw. der Poison-Gleichung bestimmt werden. Dabei nimmt t reelle Werte im Intervall [-1; 1] an mit t=cosö¡. In ihrer Definition nach Neumann-Ferrer gilt:
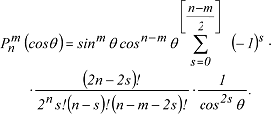 Die Bezeichnung [(n-m)/2] bedeutet hierbei (n-m)/2 fû¥r gerade n-m und (n-m-1/2) fû¥r ungerade n-m. Die Definition der Pnm ist identisch mit der Formel von Rodrigues: Die Bezeichnung [(n-m)/2] bedeutet hierbei (n-m)/2 fû¥r gerade n-m und (n-m-1/2) fû¥r ungerade n-m. Die Definition der Pnm ist identisch mit der Formel von Rodrigues:
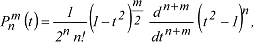 wenn man (t2-1)n nach dem binomischen Satz entwickelt und (n+m) differenziert. Fû¥r m=0 erhûÊlt man die zonalen Kugelfunktionen, fû¥r mã 0 die zugeordneten. Im allgemeinen werden in der Geophysik, insbesondere im Geomagnetismus die Kugelfunktionen in der Quasinormierung nach Adolf Schmidt bevorzugt, da somit fû¥r die hûÑheren Grade n weitgehend gleiche GrûÑssenordnungen fû¥r die Reihenentwicklungsterme (Kugelfunktionsentwicklung-SHA) erreicht werden. Die Umrechnung der Pnm nach Neumann-Ferrer in diejenigen nach Adolf Schmidt erfolgt mit dem Normierungsfaktor: wenn man (t2-1)n nach dem binomischen Satz entwickelt und (n+m) differenziert. Fû¥r m=0 erhûÊlt man die zonalen Kugelfunktionen, fû¥r mã 0 die zugeordneten. Im allgemeinen werden in der Geophysik, insbesondere im Geomagnetismus die Kugelfunktionen in der Quasinormierung nach Adolf Schmidt bevorzugt, da somit fû¥r die hûÑheren Grade n weitgehend gleiche GrûÑssenordnungen fû¥r die Reihenentwicklungsterme (Kugelfunktionsentwicklung-SHA) erreicht werden. Die Umrechnung der Pnm nach Neumann-Ferrer in diejenigen nach Adolf Schmidt erfolgt mit dem Normierungsfaktor:
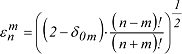 mit öÇ0m=0 fû¥r m=0 und öÇ0m=1 fû¥r mã 0, mit öÇ0m=0 fû¥r m=0 und öÇ0m=1 fû¥r mã 0,
so dass Pnm(t) (Adolf Schmidt)= önmPnm(t) (Neumann-Ferrer). |
|