| |
Koeffizienten σ2 , die sich bei der Reihenentwicklung der (Auto-)nKovarianzfunktion eines homogen-isotropen Prozesses auf der Kugel nach Legendreschen Polynomen ergeben:
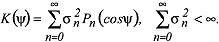 Der Winkel ψ ist der sphärische Abstand zweier Punkte auf der Einheitskugel. Die Gradvarianzen treten auch in der Norm der Laplaceschen Kugelflächenfunktionen vom Grad n auf: Der Winkel ψ ist der sphärische Abstand zweier Punkte auf der Einheitskugel. Die Gradvarianzen treten auch in der Norm der Laplaceschen Kugelflächenfunktionen vom Grad n auf:
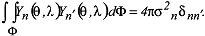 Sie stehen damit in enger Beziehung zur Spektraldarstellung einer Funktion auf der Kugel. Stellt man beispielsweise das Gravitationspotential in einer Reihe nach vollständig normierten Kugelflächenfunktionen Sie stehen damit in enger Beziehung zur Spektraldarstellung einer Funktion auf der Kugel. Stellt man beispielsweise das Gravitationspotential in einer Reihe nach vollständig normierten Kugelflächenfunktionen 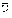
(θ,λ), 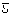
(θ,λ):
nm
nm
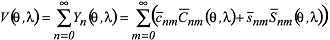 mit den vollständig normierten Potentialkoeffizienten: mit den vollständig normierten Potentialkoeffizienten:
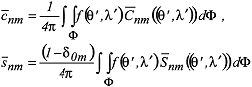 dar, so ergeben sich die Gradvarianzen aus der Formel: dar, so ergeben sich die Gradvarianzen aus der Formel:
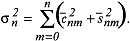 Damit kann die Kovarianzfunktion des Gravitationspotentials, betrachtet als homogen-isotroper Prozess auf der Kugel, nach der anfangs gegebenen Formel dargestellt werden. Modelle der Gradvarianzen sind bedeutsam bei der Approximation und Prädiktion physikalischer Feldfunktionen, wie beispielsweise des Gravitationspotentials. Häufig verwendet wird das von Kaula 1959 angegebene empirische globale Modell der Gradvarianzen für das Gravitationspotential ("Kaula's rule of thumb"): Damit kann die Kovarianzfunktion des Gravitationspotentials, betrachtet als homogen-isotroper Prozess auf der Kugel, nach der anfangs gegebenen Formel dargestellt werden. Modelle der Gradvarianzen sind bedeutsam bei der Approximation und Prädiktion physikalischer Feldfunktionen, wie beispielsweise des Gravitationspotentials. Häufig verwendet wird das von Kaula 1959 angegebene empirische globale Modell der Gradvarianzen für das Gravitationspotential ("Kaula's rule of thumb"):
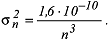 |
|