|
| |
|
| |
Herglotz-Wiechert-Verfahren |
|
| |
|
|
| |
Wiechert-Herglotz-Verfahren, Methode zur Ermittlung der radial-symmetrischen Geschwindigkeitsverteilung in der Erde aus den an der Erdoberfläche beobachteten Laufzeiten von P- und S-Wellen. Voraussetzung für die Anwendung der Methode ist, dass die seismische Geschwindigkeit V monoton mit der Tiefe z zunimmt. Ausgangspunkt des Verfahrens ist der seismische Strahlparameter p, welcher der Steigung der Laufzeitkurve in der Entfernung X entspricht (Abb. 1): p = dX/dT. Den Wert von p erhält man durch Differentiation der Laufzeitkurve oder durch direkte Messungen der Laufzeitdifferenzen an seismischen Arrays. Unter den oben genannten Voraussetzungen nimmt p monoton mit der Entfernung X ab. Das bedeutet, dass die Umkehrfunktion X(p) eindeutig ist. Für die Scheiteltiefe des Strahls, der in der Entfernung X1
auftaucht, gilt:
2
z1 =(1/π)·∫·X(p)/√(p-p12)dp. (1) Aus der Scheiteltiefe z1 lässt sich die Geschwindigkeit V(z1) ausrechnen (Benndorfscher Satz):
V(z1) =1/p1. (2) Die obigen Formeln gelten für ebene Schichtung. Man kann sie leicht auf kugelförmige Schichtung erweitern, indem man folgende Substitutionen vornimmt: X(p) durch RE·Δ(p) (Δ =Herdentfernung in Winkelgrad), Tiefe z durch RE·ln(RE/R) und Geschwindigkeit V(z) durch V(z)·ln(RE/R) ersetzen. Man geht in der Inversion so vor, dass man x1 in kleinen Schritten von der Xmin (für den bei Xmin
auftauchenden Strahl muss die Geschwindigkeit in der Scheiteltiefe bekannt sein) bis Xmax erhöht. Für jedes x1 lässt sich die Scheiteltiefe z1 durch Integration der Gleichung (1) zwischen p1 und p0 sowie die zugehörige Geschwindigkeit aus Gleichung (2) ermitteln. Damit ergibt sich die Geschwindigkeits-Tiefen-Funktion bis zu der Tiefe, die der Scheiteltiefe des Strahls entspricht, der in der Maximalentfernung Xmax auftaucht.
Das Verfahren funktioniert auch in den Fällen, in denen die Geschwindigkeit so schnell mit der Tiefe zunimmt, dass es zur Triplikation der Laufzeitkurve kommt (Abb. 2). Strahlen, die ihren Scheitelpunkt oberhalb einer solchen Übergangszone haben, tauchen mit zunehmender Scheiteltiefe in grösserer Entfernung auf. Wegen der starken Brechung in der Übergangszone kommt es zu einem rückläufigen Verlauf der Strahlen, d.h. mit zunehmender Scheiteltiefe tauchen sie in kürzeren Entfernungen auf. Sobald die Scheitelpunkte unterhalb der Übergangszone liegen, nimmt die Entfernung des Auftauchpunktes mit zunehmender Scheiteltiefe wieder zu. Die zugehörige Laufzeitkurve und Verlauf des Strahlparameters sind in Abb. 2 schematisch dargestellt. Wegen der Eindeutigkeit der Funktion X(p) lässt sich die Inversion durchführen. Hierzu benötigt man allerdings alle Äste der Triplikation. Dies erfordert die korrekte Identifizierung von späteren Phasen, was in der Praxis wegen Interferenz mit Streuphasen schwierig ist.
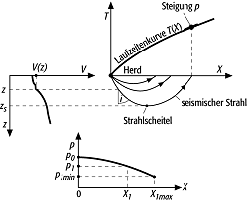 Herglotz-Wiechert-Verfahren 1: Geschwindigkeits-Tiefen-Funktion V(z), Laufzeitkurve T(X) und Strahlparameter p(X) mit X = Entfernung, p = Strahlparameter, z = Tiefe. Herglotz-Wiechert-Verfahren 1: Geschwindigkeits-Tiefen-Funktion V(z), Laufzeitkurve T(X) und Strahlparameter p(X) mit X = Entfernung, p = Strahlparameter, z = Tiefe.
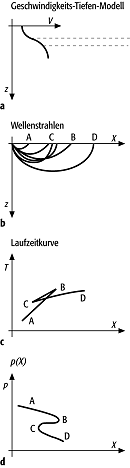 Herglotz-Wiechert-Verfahren 2: a)-d) Triplikation der Laufzeitkurve bei schneller Zunahme der Geschwindigkeit mit der Tiefe (z = Tiefe, X = Entfernung, p = Strahlparameter, T = Zeit, V = Geschwindigkeit). Herglotz-Wiechert-Verfahren 2: a)-d) Triplikation der Laufzeitkurve bei schneller Zunahme der Geschwindigkeit mit der Tiefe (z = Tiefe, X = Entfernung, p = Strahlparameter, T = Zeit, V = Geschwindigkeit). |
|
| |
|
|
| |
Ein Bookmark auf diese Seite setzen:
|
|
| |
|
|
| |
<< vorheriger Begriff |
|
nächster Begriff >> |
|
|
|
|
|
| |
|
|
|
|