| |
1) Geologie: Vorgänge, die zur Bildung von Falten führen. Abhängig vom Druck und von der Temperatur, unter der eine Falte entsteht, wirken viele verschiedene Vorgänge bei der Faltung mit: starre Blockrotation, Sprödbrüche, Drucklösung und Ausfällung, Einregelung und Neubildung von Mineralen sowie duktiles Fliessen.
2) Kristallographie: Faltungsintegral, Operation zweier Funktionen f(x) und g(x):
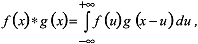 die man durch den Operator * symbolisiert. Dieses Faltungsintegral ist von fundamentaler Bedeutung für die Beschreibung der Röntgen-, Neutronen- und Elektronenbeugung an Einkristallen. Man kann es wie folgt interpretieren: a) Man invertiert g(u) und verschiebt die Funktion nach u = x (dieses "Herumfalten" der Funktion g(u) um u = x gibt der Faltung ihren Namen). b) Man multipliziert g(x-u) mit f(u) und integriert über den Wertebereich. c) Man wiederholt Schritte a) und b) für alle Werte des Definitionsbereichs (in der Praxis ist das der Bereich, in dem f(u) und g(x-u) überlappen). Das Resultat ist - Punkt für Punkt - ein mit f(x) gewichtetes Integral der Funktion g(x). die man durch den Operator * symbolisiert. Dieses Faltungsintegral ist von fundamentaler Bedeutung für die Beschreibung der Röntgen-, Neutronen- und Elektronenbeugung an Einkristallen. Man kann es wie folgt interpretieren: a) Man invertiert g(u) und verschiebt die Funktion nach u = x (dieses "Herumfalten" der Funktion g(u) um u = x gibt der Faltung ihren Namen). b) Man multipliziert g(x-u) mit f(u) und integriert über den Wertebereich. c) Man wiederholt Schritte a) und b) für alle Werte des Definitionsbereichs (in der Praxis ist das der Bereich, in dem f(u) und g(x-u) überlappen). Das Resultat ist - Punkt für Punkt - ein mit f(x) gewichtetes Integral der Funktion g(x).
3) Photogrammetrie: Filterung, Faltungsintegral, Funktion, die das Eingangssignal in ein System mit dem Ausgangssignal verbindet. Das funktionale Modell einer Faltung ist entweder eine Integralfunktion oder bei diskreten Werten eine Summenbildung. In der Photogrammetrie und Fernerkundung ist das Eingangssignal die Intensitätsmatrix eines zu filternden digitalen Bildes und das Ausgangssignal das Ergebnisbild. Die Faltung im Objektraum besteht in der Verknüpfung der Intensitätswerte innerhalb eines Operatorfensters. Mathematisch und rechentechnisch einfacher kann eine Faltung nach Transformation des Bildes in den Frequenzraum vollzogen werden (Abb.). Im Objektraum gilt für die Faltung die symbolische Schreibweise: G' = W*G,
wobei G die Matrix des Eingabebildes ist, W der Faltungsoperator bzw. die Filtermatrix und G' die Matrix des Ausgabebildes. Nach einer Fouriertransformation des Bildes vereinfacht sich die Faltung im Frequenzraum auf die Beziehung:
A'= H·A, wobei A das Amplitudenspektrum des Eingabebildes, H die Transferfunktion und A' das Amplitudenspektrum des Ausgabebildes ist. Durch eine inverse Fouriertransformation kann sowohl die Transferfunktion H in die Filtermatrix W als auch das Amplitudenspektrum A' des Ausgabebildes in die Matrix des Ausgabebildes G' überführt werden.
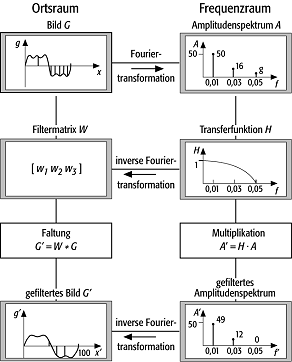
Faltung: Faltung im Orts- und Frequenzraum. |
|