| |
endlicher Bereich einer Kristallstruktur, aus dem sich durch Anwendung von Translationen (Verschiebungen) die gesamte Struktur aufbauen lässt (Tab. 1, Tab. 2). Handelt es sich um einen kleinsten Bereich mit dieser Eigenschaft, dann spricht man von einer primitiven Elementarzelle, andernfalls von einer zentrierten Zelle. Es gibt in jeder Struktur unendlich viele Möglichkeiten, eine Elementarzelle (auch eine primitive) zu wählen. Es ist Konvention, ein Parallelepiped (bzw. Parallelogramm) zu wählen und darauf zu achten, dass die Zelle der Symmetrie der Kristallstruktur möglichst gut angepasst ist und, insoweit die Symmetrie dies zulässt, rechte Winkel zwischen den Kanten besitzt. So ist in dem zweidimensionalen Punktgitter der Symmetrie c2mm die linke obere Elementarzelle wegen ihrer hohen Symmetrie und dem rechten Winkel zwischen den Kanten die in der Kristallographie bevorzugte (Abb.). In einer Kristallstruktur mit rhomboedrischen Gitter lässt sich stets auch eine hexagonale Elementarzelle wählen, wobei dann die kleinste hexagonale Zelle das dreifache Volumen der kleinsten rhomboedrischen Zelle besitzt. Umgekehrt lässt eine Struktur mit hexagonalem Gitter auch die Wahl einer dreimal so grossen rhomboedrischen Zelle zu. Hiervon wird aber selten Gebrauch gemacht, da Berechnungen im hexagonalen Koordinatensystem als einfacher empfunden werden, als solche im rhomboedrischen. Ein ausgezeichneter Punkt in einer Elementarzelle ist der Ursprung, an den die drei Basisvektoren angeheftet sind. Es ist üblich, den Ursprung in einen Punkt möglichst hoher Symmetrie zu legen und bei zentrosymmetrischen Kristallen in ein Inversionszentrum. Bei einigen Raumgruppen schliessen sich diese beiden Forderungen gegenseitig aus. Ein Beispiel ist die Raumgruppe Fd 
m des Diamants. In der Diamantstruktur liegen die Inversionszentren auf den Mittelpunkten der C-C-Bindungen mit Lagesymmetrie 
m. Die C-Atome hingegen liegen auf Punkten höherer (aber die Inversion nicht enthaltender) Symmetrie, nämlich 
3m. In solchen Fällen lässt die Konvention beide Darstellungsweisen (im Beispiel: Ursprung in 
m und Ursprung in 
3m) zu. In den niedersymmetrischen, d.h. den triklinen, monoklinen und orthorhombischen Kristallsystemen führen die durch die Symmetrie gegebenen Bedingungen noch nicht zu einer eindeutigen Wahl der Elementarzelle. Um dies zu erreichen, bedient man sich spezieller sogenannter Reduktionsverfahren. WEK Literatur: HAHN, TH. (Hrsg.)(1992): International Tables for Crystallography, Volume A, Space-Group Symmetry. - Dordrecht (Holland).
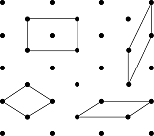 Elementarzelle: Elementarzellen im zweidimensionalen Punktgitter der Symmetrie c2mm. Elementarzelle (Tab. 1): Symmetriebedingungen der zweidimensionalen Elementarzellen. a und b sind die Beträge der Elementarzelle: Elementarzellen im zweidimensionalen Punktgitter der Symmetrie c2mm. Elementarzelle (Tab. 1): Symmetriebedingungen der zweidimensionalen Elementarzellen. a und b sind die Beträge der
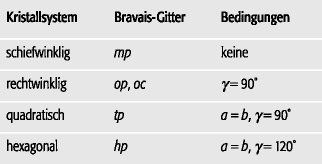 Vektoren Vektoren 
und 
; γ = ∠(
,

) der Winkel zwischen dem Vektor-Paar.
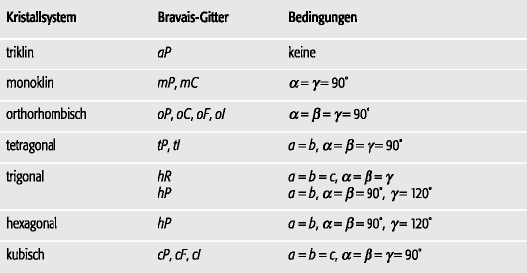 Elementarzelle (Tab. 2): Symmetriebedingungen der dreidimensionalen Elementarzellen. a, b und c sind die Beträge der Vektoren Elementarzelle (Tab. 2): Symmetriebedingungen der dreidimensionalen Elementarzellen. a, b und c sind die Beträge der Vektoren 
,

und 
; α = ∠(
,

), β = ∠(
,

) und γ = ∠(
,

) die Winkel zwischen den Vektor-Paaren. |
|