| |
in der Kristallographie Gruppe, die von einem einzigen ihrer Elemente erzeugt werden kann. Die Gruppe enthält also mindestens ein Element mit der Eigenschaft, dass alle ihre Elemente Potenzen dieses einen Elements sind. Von den 32 kristallographischen Punktgruppen des dreidimensionalen Raums sind zehn zyklisch, nämlich (in Hermann-Mauguin-Nomenklatur) 1, 2, 3, 4, 6,

,
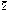
=m,

,

und 
. In Schoenflies-Nomenklatur sind das die Gruppen (in derselben Reihenfolge) C1, C2, C3, C4, C6, Ci, Cs, C3i, S4 und C3h (wobei der Buchstabe „C” für „cyclisch” steht). Neben diesen endlichen Gruppen sei als Beispiel für eine unendliche zyklische Gruppe diejenige eindimensionale Raumgruppe erwähnt, die nur aus Translationen besteht. |
|