| |
jede ganzzahlige Linearform φ:
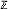
n→
auf der Menge 
n, dem n-dimensionalen Zahlengitter, lässt sich durch ein n-tupel H=(h1,h2,...,hn) ganzer Zahlen beschreiben:
φ(x1,...,xn)=h1x1+...+hnxn.
Beschreiben die n-tupel X=(x1,...,xn) die Vektoren 
eines n-dimensionalen Gitters mit Gitterbasis 1B*=( 
1,..., 
), so kann man in demselben Raum eine zweite Basis B*=( 
,..., 
n) einführen, derart,
ndass die Linearform als Skalarprodukt φ( 
)= 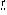
·
geschrieben werden kann, wobei 
= 
1x1+...+ 
xn
nund 
=h1 
1+...+hn 
n ist. Die Menge der Vektoren 
wird in dieser Interpretation als reziprokes Gitter bezeichnet. Die Beziehung zwischen der Basis B* des direkten Gitters und des reziproken Gitters ist gegeben durch:
j=δij=1 für i=j, sonst 0.
Aufgrund dieser Beziehung sind die physikalischen Dimensionen der Vektoren des reziproken Gitters gleich (Länge)-1, wenn die Dimension im direkten Gitter durch eine Länge ausgedrückt wird. Verwendet man (im dreidimensionalen Raum) das Vektorprodukt, so kann man die Beziehung zwischen direkter und reziproker Basis auch in der Form:

i=(1/V) 
j× 
k {i,j,k}={1,2,3} schreiben, wenn V das Volumen des von { 
1, 
2, 
3} aufgespannten Parallelepipeds (Elementarzelle) bezeichnet. Die physikalische Bedeutung des reziproken Gitters besteht darin, dass bei Beugungsexperimenten an kristalliner Materie (Röntgenbeugung, Röntgenstrukturanalyse) die Reflexe, also die geometrischen Bedingungen für konstruktive Interferenz, durch die Vektoren des zum Kristallgitter reziproken Gitters beschrieben werden. Die Richtung eines reziproken Gittervektors stimmt mit der Normalenrichtung der Netzebenenschar überein, an der man sich im Braggschen Modell die »Reflexion« der Röntgenstrahlen vorstellt. Der Netzebenenabstand d ist die reziproke Länge des kürzesten reziproken Gittervektors in dieser Richtung. Die reziproken Gittervektoren der Länge n/d beschreiben die n-te Beugungsordnung an dieser Netzebenenschar. Aus diesem Zusammenhang ergibt sich für die Kristallmorphologie, dass die Normalen von Kristallflächen Richtungen reziproker Gittervektoren markieren, während die Kanten des Kristalls Richtungen von Vektoren des Kristallgitters entsprechen. Die Millerschen Indizes sind daher die Koordinaten spezieller reziproker Gittervektoren, die Reflexionsstellungen 1. Ordnung beschreiben (Koordinaten reziproker Gittervektoren höherer Beugungsordnung sind jedoch keine Millerschen Indizes). Im Rahmen der Fouriertheorie der Distributionen erscheint das reziproke Gitter als Fouriertransformierte (Fouriertransformation) des direkten Gitters (Kristallgitters). |
|