| |
beruhen auf einem sphärischen Polarkoordinatensystem, in dem durch zwei Winkelangaben die Position eines Punktes der Erdoberfläche festgelegt wird. Diese Winkel sind die geographische Breite φ und die geographische Länge λ (Gradnetz der Erde). Geographische Koordinaten φ, λ sind ein übergeordneter allgemeiner Begriff, der nichts Definitives über die Dimensionen des Erdkörpers aussagt. Approximiert man die Erde durch eine Kugel vom mittleren Radius R = 6377,22 km, so werden gelegentlich sphärische geographische Koordinaten mit Φ und Λ bezeichnet. Bei der Verwendung eines Ellipsiods als Bezugsfläche werden die geodätische Breite und die geodätische Länge durch B und L bezeichnet (Gradnetz der Erde). Wird die Position eines Punktes A auf der Erdoberfläche durch astronomische Beobachtungen bestimmt, so spricht man von astronomischer Breite und Länge und verwendet dafür wiederum φ und λ. Dabei ist die astronomische Breite φ der Winkel zwischen der Lotrichtung in A und der Äquatorebene. Die astronomische Länge λ ist der Winkel zwischen der natürlichen Meridianebene von P und dem Greenwicher Nullmeridian. Die natürliche Meridianebene enthält den Punkt A sowie die Lotrichtung in A und steht senkrecht auf der Äquatorebene. Die Unterschiede zwischen den geodätischen (ellipsoidischen) und den astronomischen (geoidischen) Koordinaten sind Elemente für die punktweise Konstruktion der physischen Erdoberfläche, des Geoids. Die als Lotabweichungen bezeichneten Differenzen zwischen geodätischen und astronomischen (auch natürlichen) Koordinaten liegen in der Regel unter 10''.
Für geographische und kartographische Zwecke (Kartennetzentwürfe) werden die sphärischen geographischen Koordinaten den astronomischen gleichgesetzt, weshalb zur Vereinfachung die Symbole φ für die Breite und λ für die Länge verwendet werden können. Für die praktische rechnerische Handhabung ist es oft zweckmässig, die sphärischen Polarkoordinaten durch räumliche kartesische Koordinaten zu ersetzen. Es gelten dann die aus Abbildung 1 ablesbaren Beziehungen für den Vektor 
, dessen Betrag gleich dem Kugelradius R ist:
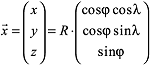 mit r = Rcosφ. mit r = Rcosφ.
Durch Anwendung von Beziehungen der sphärischen Trigonometrie kann man bei Kenntnis der geographischen Koordinaten mehrerer Punkte der Kugeloberfläche grundlegende Aufgaben der
Nautik lösen. Sind die Koordinaten φ1, λ1 des Punktes A1 und φ2, λ2 des Punktes A2 gegeben, so
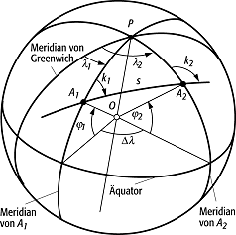
kann man mit dem Pol P als drittem Punkt ein sphärisches Dreieck (Poldreieck) bilden, in dem Entfernungen und Winkel auf der Kugeloberfläche berechenbar sind. In Abbildung 2 gelten die bereits verwendeten Symbole. Der Bogen s, der sphärische Abstand zwischen A1 und A2, ist ein Teil des Grosskreises und damit die kürzeste Verbindung der beiden Punkte, die als Orthodrome bezeichnet wird. Die Bogenlänge wird mit dem sphärischen Kosinussatz berechnet: coss =sinφ1·sinφ2+cosφ1·cosφ1·cosφ2·cosΔλ mit Δλ = λ2 -λ1.
Die Kurswinkel (Abb. 2) sind die Schnittwinkel k1 und k2 des Grosskreisbogens mit den Meridianen von A1 und A2. Sie können mit dem sphärischen Sinussatz berechnet werden:
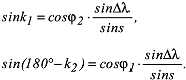 KGS KGS
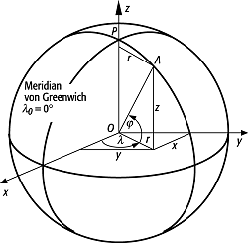 geographische Koordinaten 1: rechtwinklige Koordinaten eines Kugelpunktes. geographische Koordinaten 1: rechtwinklige Koordinaten eines Kugelpunktes.
 geographische Koordinaten 2: sphärisches Dreieck.f einem sphärischen Polarkoordinatensystem, in dem durch zwei Winkelangaben die Position eines Punktes der Erdoberfläche festgelegt wird. Diese Winkel sind die geographische Breite φ und die geographische Länge λ (Gradnetz der Erde). Geographische Koordinaten φ, λ sind ein übergeordneter allgemeiner Begriff, der nichts Definitives über die Dimensionen des Erdkörpers aussagt. Approximiert man die Erde durch eine Kugel vom mittleren Radius R = 6377,22 km, so werden gelegentlich sphärische geographische Koordinaten mit Φ und Λ bezeichnet. Bei der Verwendung eines Ellipsiods als Bezugsfläche werden die geodätische Breite und die geodätische Länge durch B und L bezeichnet (Gradnetz der Erde). Wird die Position eines Punktes A auf der Erdoberfläche durch astronomische Beobachtungen bestimmt, so spricht man von astronomischer Breite und Länge und verwendet dafür wiederum φ und λ. Dabei ist die astronomische Breite φ der Winkel zwischen der Lotrichtung in A und der Äquatorebene. Die astronomische Länge λ ist der Winkel zwischen der natürlichen Meridianebene von P und dem Greenwicher Nullmeridian. Die natürliche Meridianebene enthält den Punkt A sowie die Lotrichtung in A und steht senkrecht auf der Äquatorebene. Die Unterschiede zwischen den geodätischen (ellipsoidischen) und den astronomischen (geoidischen) Koordinaten sind Elemente für die punktweise Konstruktion der physischen Erdoberfläche, des Geoids. Die als Lotabweichungen bezeichneten Differenzen zwischen geodätischen und astronomischen (auch natürlichen) Koordinaten liegen in der Regel unter 10''. geographische Koordinaten 2: sphärisches Dreieck.f einem sphärischen Polarkoordinatensystem, in dem durch zwei Winkelangaben die Position eines Punktes der Erdoberfläche festgelegt wird. Diese Winkel sind die geographische Breite φ und die geographische Länge λ (Gradnetz der Erde). Geographische Koordinaten φ, λ sind ein übergeordneter allgemeiner Begriff, der nichts Definitives über die Dimensionen des Erdkörpers aussagt. Approximiert man die Erde durch eine Kugel vom mittleren Radius R = 6377,22 km, so werden gelegentlich sphärische geographische Koordinaten mit Φ und Λ bezeichnet. Bei der Verwendung eines Ellipsiods als Bezugsfläche werden die geodätische Breite und die geodätische Länge durch B und L bezeichnet (Gradnetz der Erde). Wird die Position eines Punktes A auf der Erdoberfläche durch astronomische Beobachtungen bestimmt, so spricht man von astronomischer Breite und Länge und verwendet dafür wiederum φ und λ. Dabei ist die astronomische Breite φ der Winkel zwischen der Lotrichtung in A und der Äquatorebene. Die astronomische Länge λ ist der Winkel zwischen der natürlichen Meridianebene von P und dem Greenwicher Nullmeridian. Die natürliche Meridianebene enthält den Punkt A sowie die Lotrichtung in A und steht senkrecht auf der Äquatorebene. Die Unterschiede zwischen den geodätischen (ellipsoidischen) und den astronomischen (geoidischen) Koordinaten sind Elemente für die punktweise Konstruktion der physischen Erdoberfläche, des Geoids. Die als Lotabweichungen bezeichneten Differenzen zwischen geodätischen und astronomischen (auch natürlichen) Koordinaten liegen in der Regel unter 10''.
Für geographische und kartographische Zwecke (Kartennetzentwürfe) werden die sphärischen geographischen Koordinaten den astronomischen gleichgesetzt, weshalb zur Vereinfachung die Symbole φ für die Breite und λ für die Länge verwendet werden können. Für die praktische rechnerische Handhabung ist es oft zweckmässig, die sphärischen Polarkoordinaten durch räumliche kartesische Koordinaten zu ersetzen. Es gelten dann die aus Abbildung 1 ablesbaren Beziehungen für den Vektor 
, dessen Betrag gleich dem Kugelradius R ist:
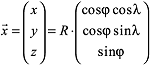 mit r = Rcosφ. mit r = Rcosφ.
Durch Anwendung von Beziehungen der sphärischen Trigonometrie kann man bei Kenntnis der geographischen Koordinaten mehrerer Punkte der Kugeloberfläche grundlegende Aufgaben der
Nautik lösen. Sind die Koordinaten φ1, λ1 des Punktes A1 und φ2, λ2 des Punktes A2 gegeben, so
kann man mit dem Pol P als drittem Punkt ein sphärisches Dreieck (Poldreieck) bilden, in dem Entfernungen und Winkel auf der Kugeloberfläche berechenbar sind. In Abbildung 2 gelten die bereits verwendeten Symbole. Der Bogen s, der sphärische Abstand zwischen A1 und A2, ist ein Teil des Grosskreises und damit die kürzeste Verbindung der beiden Punkte, die als Orthodrome bezeichnet wird. Die Bogenlänge wird mit dem sphärischen Kosinussatz berechnet: coss =sinφ1·sinφ2+cosφ1·cosφ1·cosφ2·cosΔλ mit Δλ = λ2 -λ1.
Die Kurswinkel (Abb. 2) sind die Schnittwinkel k1 und k2 des Grosskreisbogens mit den Meridianen von A1 und A2. Sie können mit dem sphärischen Sinussatz berechnet werden:
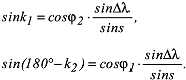 KGS KGS
 geographische Koordinaten 1: rechtwinklige Koordinaten eines Kugelpunktes. geographische Koordinaten 1: rechtwinklige Koordinaten eines Kugelpunktes.
 geographische Koordinaten 2: sphärisches Dreieck. geographische Koordinaten 2: sphärisches Dreieck. |
|