| |
gleichzeitige Bestimmung mehrerer Grössen des astronomischen Dreiecks (Breite, Länge und/oder Azimut) aus Sternbeobachtungen. Am bekanntesten ist die Höhenstandlinienmethode, die zur simultanen Bestimmung von astronomischer Länge und Breite eines Ortes auf der Erdoberfläche dient. Die Zenitdistanz zi mehrerer Sterne Si in unterschiedlichen Azimuten wird gemessen bei gleichzeitiger Registrierung der Zeit UTC. Bei bekannten Sternkoordinaten αi, δi wird durch die gemessene Zenitdistanz ein Raumvektor bestimmt, der vom Stern ausgehend die Erdoberfläche im Beobachtungsort B erreicht. B liegt auf einem Kleinkreis der Erdkugel, dessen Mittelpunkt derjenige Erdort ist, in dem der Stern Si im Beobachtungsmoment im Zenit steht. Zur eindeutigen Bestimmung der Position des Punktes B (Φ,Λ) benötigt man drei solcher Kleinkreise oder Positionskreise, die in B einen gemeinsamen Schnittpunkt haben. Praktisch löst man die Aufgabe differentiell, wenn man Näherungskoordinaten von B (Φ0,Λ0) hat. In ein ebenes, nach Norden orientiertes Koordinatensystem x, y, das der quadratischen Plattkarte (Zylinderentwürfe) in einem vorzugebenden Massstab entspricht, wird der „gegisste” Ort B0 als Mittelpunkt eingetragen. Bei bekannten Näherungkoordinaten genügt die Beobachtung von zwei Sternen Si. Die graphische Lösung der Ortsbestimmungsaufgabe erfolgt wie in der Abbildung dargestellt. Unter den Azimuten Ai werden die Richtungen nach den Sternen Si aufgetragen. Da B0 nur genähert mit dem gesuchten Punkt B zusammenfällt, werden die Positionskreise sich nicht in B0, sondern in B‘ schneiden. Dieser Punkt wird gefunden, indem man die Positionskreise durch die als Standlinien 1 und 2 bezeichneten Tangenten ersetzt. Die Standlinien stehen senkrecht auf den Richtungen B0Si. Ihr Abstand Δzi von B0 ist gleich der Differenz zwischen zi, der gemessen wird, und z0i, der aus den Sternkoordinaten und den Näherungswerten der Standortkoordinaten berechneten Zenitdistanz. Die aus der simultanen astronomischen Ortsbestimmung abgeleiteten Koordinaten des Beobachtungsortes B sind:
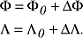 ΔΦ und ΔΛcosΦ0 werden aus der Graphik abgegriffen, wie in der Abbildung gezeigt. Hat man mehr als zwei Sterne Si beobachtet, entsteht eine fehlerzeigende Figur, deren Inkreismittelpunkt B‘ entspricht. Im Fall mehrerer beobachteter Sterne empfiehlt sich eine vermittelnde Ausgleichung zur Bestimmung von ΔΦ und ΔΛ. ΔΦ und ΔΛcosΦ0 werden aus der Graphik abgegriffen, wie in der Abbildung gezeigt. Hat man mehr als zwei Sterne Si beobachtet, entsteht eine fehlerzeigende Figur, deren Inkreismittelpunkt B‘ entspricht. Im Fall mehrerer beobachteter Sterne empfiehlt sich eine vermittelnde Ausgleichung zur Bestimmung von ΔΦ und ΔΛ.
Eine wichtige Variante dieses Verfahrens benutzt n > 3 Sterne in einer konstanten Höhe, also in zirkumzenitaler Position. Für diese Methode gleicher Höhen wurden spezielle Instrumente mit konstruktiv festgelegten Beobachtungshöhen gebaut, z.B. Prismenastrolabien, transportable Zenitkameras u.a. Die Azimute der n Sterne sollen gleichmässig über den Horizont verteilt sein. Nach den Differentialformeln (1) und (3) der astronomischen Ortsbestimmung tragen zirkummeridiane Sterne am meisten zur Genauigkeit der Breite Φ und Sterne nahe dem I. Vertikal (Ost- und Weststerne) am meisten zur Genauigkeit der Länge Λ (bzw. der Zeit) bei.
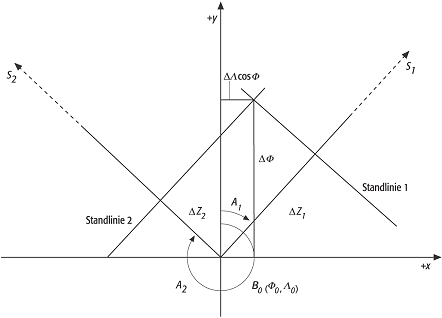 simultane astronomische Ortsbestimmung: differentielle Lösung der simultanen astronomischen Ortsbestimmung nach der Höhenstandlinienmethode. simultane astronomische Ortsbestimmung: differentielle Lösung der simultanen astronomischen Ortsbestimmung nach der Höhenstandlinienmethode. |
|