| |
notwendige Bedingungen für das Auftreten eines abgebeugten Strahls bei der Streuung von Elektronen-, Neutronen- oder Röntgenstrahlen an Kristallen. Diese Strahlen wechselwirken mit den im Kristall dreidimensional periodisch (Translationssymmetrie) angeordneten Atomkernen und Atomelektronen und werden gestreut. Die Überlagerung der von den Streuern ausgehenden Sekundärwellen, die untereinander feste, zeitunabhängige Phasendifferenzen haben (kohärente Streuung), die ihrerseits vom Abstand der Streuer und vom Streuwinkel abhängen, ergibt maximale resultierende Amplitude (Interferenz-, Beugungsmaximum), wenn die folgenden Gleichungen gleichzeitig erfüllt sind:
 · · 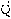
=2πh; 
· 
=2πk; 
· 
=2πl.
Dabei sind 
,

,

die Basisvektoren, die das Kristallgitter aufspannen.

ist der Differenzvektor zwischen den Wellenvektoren 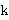
0 der einfallenden und 
der gebeugten Welle (Impulsübertrag):

=
 - -
0, dabei gilt für die hier vorausgesetzte elastische Streuung | 
|=| 
0| =2π/λ. h,k,l sind ganze Zahlen. Damit 
die Gleichungen gleichzeitig erfüllt, muss 
ein Vektor des reziproken Gitters sein:
 =2π =2π
 mit mit

= h 
*+k 
*+l 
*.

*,

*,

* sind die Basisvektoren des reziproken Gitters. Die Laue-Gleichungen besagen, dass konstruktive Interferenz, d.h. ein Beugungsmaximum, genau dann auftritt, wenn die Gangunterschiede (Wegdifferenzen) der Strahlen, die an translationsäquivalenten,
in Richtung der Basisvektoren 
,

,

benachbarten Streuern gestreut werden, ganzzahlige Vielfache h,k,l der Wellenlänge sind (Abb.). Sind diese Bedingungen nicht simultan erfüllt, dann löschen sich die gestreuten Wellen durch Interferenz gegenseitig weitgehend aus. Denkt man sich den Kristall als unendlich ausgedehnt, so ist die Auslöschung zwischen den Beugungsmaxima vollständig und die Beugungsmaxima selbst sind δ-funktionsförmig scharf.
Jedes Beugungsmaximum (Braggreflex) ist also durch ein Tripel h,k,l ganzer Zahlen, das sind die jeweiligen Beugungsordnungen für die Gitterrichtungen 
,

,

, eindeutig gekennzeichnet. Eine äquivalente Bedingung gilt für die Beugung von Licht an einem eindimensionalen Strichgitter mit dem Unterschied, dass im Kristall eine dreidimensional periodische Anordnung der Streuer vorliegt. Aus den Laue-Gleichungen folgt die Braggsche Bedingung für konstruktive Interferenzreflexion (Braggsche Gleichung) an der Netzebenenschar mit den teilerfremden Millerschen Indizes h',k',l'. Tritt in dem Tripel h, k, l ein gemeinsamer Teiler n auf, so gilt: (h',k',l')=(h,k,l)/n, d.h. es handelt sich nach der Interpretation von Bragg um einen Reflex an der Netzebenenschar mit den Millerschen Indizes h',k',l' der Ordnung n.
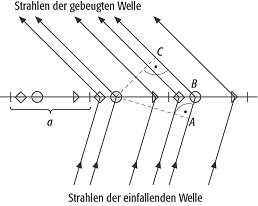 Laue-Gleichungen: schematische Darstellung der Beugung an einer eindimensionalen, translationsperiodischen Struktur mit der Translationsperiode a aus drei unterschiedlichen Streuern (Quadrat, Dreieck, Kreis) zur Interpretation der ersten Laue-Gleichungen: schematische Darstellung der Beugung an einer eindimensionalen, translationsperiodischen Struktur mit der Translationsperiode a aus drei unterschiedlichen Streuern (Quadrat, Dreieck, Kreis) zur Interpretation der ersten
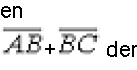 Laue-Gleichung. Zur Entstehung eines Beugungsmaximums (konstruktive Interferenz) muss der Gangunterschied Strahlen benachbarter, translationsäquivalenter Streuer ein ganzzahliges Vielfaches h der Wellenlänge sein. Bedingungen für das Auftreten eines abgebeugten Strahls bei der Streuung von Elektronen-, Neutronen- oder Röntgenstrahlen an Kristallen. Diese Strahlen wechselwirken mit den im Kristall dreidimensional periodisch (Translationssymmetrie) angeordneten Atomkernen und Atomelektronen und werden gestreut. Die Überlagerung der von den Streuern ausgehenden Sekundärwellen, die untereinander feste, zeitunabhängige Phasendifferenzen haben (kohärente Streuung), die ihrerseits vom Abstand der Streuer und vom Streuwinkel abhängen, ergibt maximale resultierende Amplitude (Interferenz-, Beugungsmaximum), wenn die folgenden Gleichungen gleichzeitig erfüllt sind: Laue-Gleichung. Zur Entstehung eines Beugungsmaximums (konstruktive Interferenz) muss der Gangunterschied Strahlen benachbarter, translationsäquivalenter Streuer ein ganzzahliges Vielfaches h der Wellenlänge sein. Bedingungen für das Auftreten eines abgebeugten Strahls bei der Streuung von Elektronen-, Neutronen- oder Röntgenstrahlen an Kristallen. Diese Strahlen wechselwirken mit den im Kristall dreidimensional periodisch (Translationssymmetrie) angeordneten Atomkernen und Atomelektronen und werden gestreut. Die Überlagerung der von den Streuern ausgehenden Sekundärwellen, die untereinander feste, zeitunabhängige Phasendifferenzen haben (kohärente Streuung), die ihrerseits vom Abstand der Streuer und vom Streuwinkel abhängen, ergibt maximale resultierende Amplitude (Interferenz-, Beugungsmaximum), wenn die folgenden Gleichungen gleichzeitig erfüllt sind:
 · · 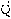
=2πh; 
· 
=2πk; 
· 
=2πl.
Dabei sind 
,

,

die Basisvektoren, die das Kristallgitter aufspannen.

ist der Differenzvektor zwischen den Wellenvektoren 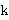
0 der einfallenden und 
der gebeugten Welle (Impulsübertrag):

=
 - -
0, dabei gilt für die hier vorausgesetzte elastische Streuung | 
|=| 
0| =2π/λ. h,k,l sind ganze Zahlen. Damit 
die Gleichungen gleichzeitig erfüllt, muss 
ein Vektor des reziproken Gitters sein:
 =2π =2π
 mit mit

= h 
*+k 
*+l 
*.

*,

*,

* sind die Basisvektoren des reziproken Gitters. Die Laue-Gleichungen besagen, dass konstruktive Interferenz, d.h. ein Beugungsmaximum, genau dann auftritt, wenn die Gangunterschiede (Wegdifferenzen) der Strahlen, die an translationsäquivalenten,
in Richtung der Basisvektoren 
,

,

benachbarten Streuern gestreut werden, ganzzahlige Vielfache h,k,l der Wellenlänge sind (Abb.). Sind diese Bedingungen nicht simultan erfüllt, dann löschen sich die gestreuten Wellen durch Interferenz gegenseitig weitgehend aus. Denkt man sich den Kristall als unendlich ausgedehnt, so ist die Auslöschung zwischen den Beugungsmaxima vollständig und die Beugungsmaxima selbst sind δ-funktionsförmig scharf.
Jedes Beugungsmaximum (Braggreflex) ist also durch ein Tripel h,k,l ganzer Zahlen, das sind die jeweiligen Beugungsordnungen für die Gitterrichtungen 
,

,

, eindeutig gekennzeichnet. Eine äquivalente Bedingung gilt für die Beugung von Licht an einem eindimensionalen Strichgitter mit dem Unterschied, dass im Kristall eine dreidimensional periodische Anordnung der Streuer vorliegt. Aus den Laue-Gleichungen folgt die Braggsche Bedingung für konstruktive Interferenzreflexion (Braggsche Gleichung) an der Netzebenenschar mit den teilerfremden Millerschen Indizes h',k',l'. Tritt in dem Tripel h, k, l ein gemeinsamer Teiler n auf, so gilt: (h',k',l')=(h,k,l)/n, d.h. es handelt sich nach der Interpretation von Bragg um einen Reflex an der Netzebenenschar mit den Millerschen Indizes h',k',l' der Ordnung n.
 Laue-Gleichungen: schematische Darstellung der Beugung an einer eindimensionalen, translationsperiodischen Struktur mit der Translationsperiode a aus drei unterschiedlichen Streuern (Quadrat, Dreieck, Kreis) zur Interpretation der ersten Laue-Gleichungen: schematische Darstellung der Beugung an einer eindimensionalen, translationsperiodischen Struktur mit der Translationsperiode a aus drei unterschiedlichen Streuern (Quadrat, Dreieck, Kreis) zur Interpretation der ersten
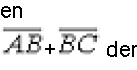 Laue-Gleichung. Zur Entstehung eines Beugungsmaximums (konstruktive Interferenz) muss der Gangunterschied Strahlen benachbarter, translationsäquivalenter Streuer ein ganzzahliges Vielfaches h der Wellenlänge sein. Laue-Gleichung. Zur Entstehung eines Beugungsmaximums (konstruktive Interferenz) muss der Gangunterschied Strahlen benachbarter, translationsäquivalenter Streuer ein ganzzahliges Vielfaches h der Wellenlänge sein. |
|