| |
Theorie der Raum- bzw. Flächenkurven. Grundlage der Kurventheorie sind die Ableitungsgleichungen für das Frenetsche Dreibein ( 
1,

3) einer Raumkurve (Frenetsche 2, Formeln):
 
'= κ· 
2,
 '=-κ· '=-κ· 
1+τ· 
3,
'=-τ· 3

2 und für das Darbouxsche Dreibein ( 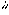
1, 
2, 
3) einer Flächenkurve (Formeln von Burali-Forti): 1 ' = κg · 2+κn · 3,
2 ' = -κ· 1+τg · 3,
2 ' = -κn · 1 -τg · 2.
(' bezeichnet die Ableitung nach der Bogenlänge s). Die in den Frenetschen Formeln auftretenden Koeffizienten sind die Krümmungκ und die Windung τ der Raumkurve; die Koeffizienten in den Formeln von Burali-Forti bezeichnet man als Normalkrümmung κn, geodätische Krümmung κg und geodätische Torsion τg der Flächenkurve. Zwischen diesen Koeffizienten bestehen enge Beziehungen; mit dem Winkel φ zwischen 2 und 3 gilt:
κn= κ·cosφ (Satz von Meusnier) κn= κ·sinφ,
τg= τ+dφ/ds.
In der Theorie der Landesvermessung wird die Kurventheorie auf Flächenkurven angewandt, die auf der Oberfläche eines Rotationsellipsoids definiert sind. Schneidet man das Rotationsellipsoid mit einer Ebene, die in einem festen Punkt P der Ellipsoidfläche die Flächennormale enthält, so nennt man die entstehende ebene Schnittkurve einen (ellipsoidischen) Normalschnitt; in P gilt φ=0 und somit κg=0. Flächenkurven, deren gesamter Verlauf durch die Eigenschaft κg≡0 charakterisiert ist, heissen geodätische Linie. In jedem Punkt einer geodätischen Linie liegt ein Normalschnitt vor, so dass die geodätischen Linien die "geradesten" Kurven auf einer gekrümmten Fläche sind. Die kürzeste, stetig gekrümmte Verbindungslinie zwischen zwei Punkten auf dem Rotationsellipsoid ist stets eine geodätische Linie.r Raum- bzw. Flächenkurven. Grundlage der Kurventheorie sind die Ableitungsgleichungen für das Frenetsche Dreibein ( 
1,

3) einer Raumkurve (Frenetsche 2, Formeln):
 
'= κ· 
2,
 '=-κ· '=-κ· 
1+τ· 
3,
'=-τ· 3

2 und für das Darbouxsche Dreibein ( 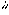
1, 
2, 
3) einer Flächenkurve (Formeln von Burali-Forti): 1 ' = κg · 2+κn · 3,
2 ' = -κ· 1+τg · 3,
2 ' = -κn · 1 -τg · 2.
(' bezeichnet die Ableitung nach der Bogenlänge s). Die in den Frenetschen Formeln auftretenden Koeffizienten sind die Krümmungκ und die Windung τ der Raumkurve; die Koeffizienten in den Formeln von Burali-Forti bezeichnet man als Normalkrümmung κn, geodätische Krümmung κg und geodätische Torsion τg der Flächenkurve. Zwischen diesen Koeffizienten bestehen enge Beziehungen; mit dem Winkel φ zwischen 2 und 3 gilt:
κn= κ·cosφ (Satz von Meusnier) κn= κ·sinφ,
τg= τ+dφ/ds.
In der Theorie der Landesvermessung wird die Kurventheorie auf Flächenkurven angewandt, die auf der Oberfläche eines Rotationsellipsoids definiert sind. Schneidet man das Rotationsellipsoid mit einer Ebene, die in einem festen Punkt P der Ellipsoidfläche die Flächennormale enthält, so nennt man die entstehende ebene Schnittkurve einen (ellipsoidischen) Normalschnitt; in P gilt φ=0 und somit κg=0. Flächenkurven, deren gesamter Verlauf durch die Eigenschaft κg≡0 charakterisiert ist, heissen geodätische Linie. In jedem Punkt einer geodätischen Linie liegt ein Normalschnitt vor, so dass die geodätischen Linien die "geradesten" Kurven auf einer gekrümmten Fläche sind. Die kürzeste, stetig gekrümmte Verbindungslinie zwischen zwei Punkten auf dem Rotationsellipsoid ist stets eine geodätische Linie. |
|