| |
von Cooper & Jacob 1946 entwickelt, beinhaltet einfache graphische Methoden, um Pumpversuche in gespannten Grundwasserleitern auszuwerten und somit die Transmissivität T und den Speicherkoeffizient S zu berechnen. Sie basieren auf der Vereinfachung der Brunnenformel von Theis. Die Theissche Brunnenfunktion:
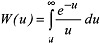 mit mit
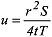 (r = Abstand Brunnen Messstelle [m], S =Speicherkoeffizient, t =Zeit seit Pumpbeginn [s], T = Transmissivität [m2/s]) kann durch eine konvergierende Reihenentwicklung ersetzt werden: (r = Abstand Brunnen Messstelle [m], S =Speicherkoeffizient, t =Zeit seit Pumpbeginn [s], T = Transmissivität [m2/s]) kann durch eine konvergierende Reihenentwicklung ersetzt werden:
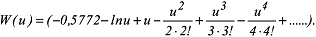 Für u ≤ 0,02 können alle Reihenglieder nach ln u vernachlässigt werden, da ihre Summe gegen Null geht. Somit erhält man die vereinfachte Theissche Brunnenformel: Für u ≤ 0,02 können alle Reihenglieder nach ln u vernachlässigt werden, da ihre Summe gegen Null geht. Somit erhält man die vereinfachte Theissche Brunnenformel:
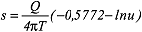 (s = Absenkung des Wasserspiegels [m], Q = Pumprate im Entnahmebrunnen [m3/s]), die sich umformen und vereinfachen lässt zu: (s = Absenkung des Wasserspiegels [m], Q = Pumprate im Entnahmebrunnen [m3/s]), die sich umformen und vereinfachen lässt zu:
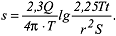 Diese Gleichung ist die Grundlage für die drei Geradlinienverfahren. a) Zeit-Absenkungsverfahren: Für eine Grundwassermessstelle wird die gemessene Absenkung s gegen lg t auftragen. Für die praktische Anwendung ist es einfacher s gegen t auf halblogarithmischem Papier aufzutragen. Da alle in der Gleichung vorkommenden Variablen bis auf s und t bei einem Pumpversuch konstant sein müssen, gibt es einen linearen Zusammenhang zwischen diesen beiden Grössen, so dass man eine Ausgleichsgerade durch die eingezeichneten Messwerte legen kann. Für eine logarithmische Dekade (z.B. zwischen 100 s und 1000 s) wird nun die Absenkungsdifferenz Δs bestimmt und hiermit die Transmissivität nach: Diese Gleichung ist die Grundlage für die drei Geradlinienverfahren. a) Zeit-Absenkungsverfahren: Für eine Grundwassermessstelle wird die gemessene Absenkung s gegen lg t auftragen. Für die praktische Anwendung ist es einfacher s gegen t auf halblogarithmischem Papier aufzutragen. Da alle in der Gleichung vorkommenden Variablen bis auf s und t bei einem Pumpversuch konstant sein müssen, gibt es einen linearen Zusammenhang zwischen diesen beiden Grössen, so dass man eine Ausgleichsgerade durch die eingezeichneten Messwerte legen kann. Für eine logarithmische Dekade (z.B. zwischen 100 s und 1000 s) wird nun die Absenkungsdifferenz Δs bestimmt und hiermit die Transmissivität nach:
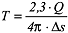 berechnet. Verlängert man nun die Ausgleichsgerade, bis sie die Zeitachse bei s =0 schneidet, so erhält man den Zeitpunkt t0. Setzt man den abgelesenen Wert für t0 in die Gleichung: berechnet. Verlängert man nun die Ausgleichsgerade, bis sie die Zeitachse bei s =0 schneidet, so erhält man den Zeitpunkt t0. Setzt man den abgelesenen Wert für t0 in die Gleichung:
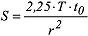 ein, so lässt sich hiermit der Speicherkoeffizient S bestimmen. Am Schluss der Auswertung muss nun mit den ermittelten Werten für S und T die Bedingung u ≤ 0,02 überprüft werden. Ist sie nicht erfüllt, wird das Verfahren für kleinere Abstände r oder spätere Zeitpunkte wiederholt. ein, so lässt sich hiermit der Speicherkoeffizient S bestimmen. Am Schluss der Auswertung muss nun mit den ermittelten Werten für S und T die Bedingung u ≤ 0,02 überprüft werden. Ist sie nicht erfüllt, wird das Verfahren für kleinere Abstände r oder spätere Zeitpunkte wiederholt.
b) Abstand-Absenkungsverfahren: Gibt es mehrere Grundwassermessstellen, die bei der Durchführung des Pumpversuchs eine Absenkung des Wasserspiegels aufweisen, kann das Abstand-Absenkungsverfahren angewendet werden. Hierbei werden für einen bestimmten Zeitpunkt t die Absenkungsbeträge s der einzelnen Messstellen gegen den Abstand r der jeweiligen Messstelle vom Entnahmebrunnen auf halblogarithmisches Papier aufgetragen und eine Ausgleichsgerade durch die Messwerte gelegt. Für eine logarithmische Dekade wird dann die Absenkungsdifferenz Δs bestimmt und hiermit die Transmissivität:
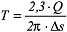 berechnet. Diese Gleichung ist identisch mit der Brunnengleichung von G. Thiem für gespannte Grundwasserleiter und stationäre Strömungsbedingungen. Verlängert man nun die Ausgleichsgerade, bis sie die Abstandsachse bei s = 0 schneidet, so erhält man den Abstand r0. Setzt man den abgelesenen Wert für r0 in die Gleichung: berechnet. Diese Gleichung ist identisch mit der Brunnengleichung von G. Thiem für gespannte Grundwasserleiter und stationäre Strömungsbedingungen. Verlängert man nun die Ausgleichsgerade, bis sie die Abstandsachse bei s = 0 schneidet, so erhält man den Abstand r0. Setzt man den abgelesenen Wert für r0 in die Gleichung:
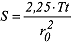 ein, so kann hiermit der Speicherkoeffizient S berechnet werden. Auch bei diesem Verfahren muss man am Ende der Berechnung die Bedingung u ≤ 0,02 überprüfen. ein, so kann hiermit der Speicherkoeffizient S berechnet werden. Auch bei diesem Verfahren muss man am Ende der Berechnung die Bedingung u ≤ 0,02 überprüfen.
c) Abstand-Zeit-Absenkungsverfahren: Da zwischen der Absenkung s und dem Logarithmus der Zeit t als auch dem Logarithmus des Abstandes r bzw. r2 ein linearer Zusammenhang besteht, so existiert dieser auch zwischen s und dem Logarithmus von t/r2. Wird s gegen t/r2 für mehrere Messstellen auf halblogarithmischem Papier aufgetragen so kann für alle Messwertpaare eine gemeinsame Ausgleichsgerade eingezeichnet werden. Genau wie bei den beiden ersten Verfahren wird nun für eine logarithmische Dekade die Absenkungsdifferenz Δs bestimmt und hiermit die Transmissivität:
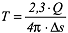 berechnet. Verlängert man die Ausgleichsgerade bis sie die t/r2-Achse bei s = 0 schneidet, erhält man den Wert für (t/r2)0, der mittels der Gleichung: berechnet. Verlängert man die Ausgleichsgerade bis sie die t/r2-Achse bei s = 0 schneidet, erhält man den Wert für (t/r2)0, der mittels der Gleichung:
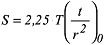 die Berechnung des Speicherkoeffizienten S ermöglicht. Abschliessend ist die Bedingung u ≤ 0,02 zu überprüfen. die Berechnung des Speicherkoeffizienten S ermöglicht. Abschliessend ist die Bedingung u ≤ 0,02 zu überprüfen.
Literatur: [1] DAWSON, K.J. & ISTOK, J.D. (1991): Aquifer Testing. Design and Analysis of Pumping and Slug Tests. - Chelsea. [2] LANGGUTH, H.-R. & VOIGT, R. (1980): Hydrogeologische Methoden.
-Berlin, Heidelberg, New York. |
|