| |
erhält man ausgehend von der Gleichung 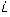
= ∂ 
/∂t+ 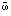
× 
, die die zeitliche Änderung des Drehimpulses
in einem körperfesten System in bezug bringt zum Drehmoment 
. Für ein Hauptträgheitsachsensystem mit den Trägheitsmomenten A, B, C gilt: A 1+(C-B)ω2ω3 = L1 B 2+(A-C)ω3ω1 = L2 A 3+(B-A)ω1ω2 = L3. Die Eulerschen Gleichungen sind der Ausgangspunkt für die Beschreibung einer Kreiselbewegung. Sie bilden ein System gewöhnlicher, gekoppelter Differentialgleichungen erster Ordnung für die Koordinaten ωi(t) des Drehvektors eines als starr angenommenen Teilchensystems. Als solches wird,
in erster Näherung, die Erde betrachtet.n ausgehend von der Gleichung 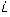
= ∂ 
/∂t+ 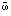
× 
, die die zeitliche Änderung des Drehimpulses
in einem körperfesten System in bezug bringt zum Drehmoment 
. Für ein Hauptträgheitsachsensystem mit den Trägheitsmomenten A, B, C gilt: A 1+(C-B)ω2ω3 = L1 B 2+(A-C)ω3ω1 = L2 A 3+(B-A)ω1ω2 = L3. Die Eulerschen Gleichungen sind der Ausgangspunkt für die Beschreibung einer Kreiselbewegung. Sie bilden ein System gewöhnlicher, gekoppelter Differentialgleichungen erster Ordnung für die Koordinaten ωi(t) des Drehvektors eines als starr angenommenen Teilchensystems. Als solches wird,
in erster Näherung, die Erde betrachtet. |
|