| |
ermöglicht im Bereich der Hydrodynamik die mathematische Beschreibung der Bewegung einer Flüssigkeit über die Zeit. Im Gegensatz zur Eulerschen Bewegungsgleichung, die die Flüssigkeitsbewegung in einem festen, durchströmten Punkt beschreibt, wird bei der Lagrangesche Betrachtungsweise die Bewegung eines einzelnen Punktes der Flüssigkeit, z.B. eines Wassermoleküls im Raum, im Hinblick auf seine Bewegungsbahn, seine Geschwindigkeit und Beschleunigung betrachtet.
Die Lagrangesche Gleichung dient dazu, den Bewegungszustand eines Flüssigkeitsteilchens während der Zeit, in der es sich auf seiner Bahn bewegt, zu bestimmen. Die Bahn wird dabei festgelegt durch die Raumkoordinaten (x0, y0, z0) zur Zeit t=0 und die Bahnkoordinaten (x, y, z) zur Zeit t. X, Y und Z sind die Beschleunigungen in den drei Raumrichtungen. Die Lagrangesche Gleichung für die x-Richtung lautet damit:
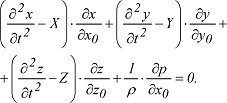 Setzt man für die Beschleunigungen K ={X,Y,Z} und für x, y und z den Ortsvektor r ={x,y,z} vereinfacht sich die Gleichung zu: Setzt man für die Beschleunigungen K ={X,Y,Z} und für x, y und z den Ortsvektor r ={x,y,z} vereinfacht sich die Gleichung zu:
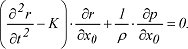 Entsprechendes gilt für die y- und z-Richtung. Für alle drei Raumrichtungen lautet die Lagrangesche Gleichung in der vereinfachten Matrix-Schreibweise: Entsprechendes gilt für die y- und z-Richtung. Für alle drei Raumrichtungen lautet die Lagrangesche Gleichung in der vereinfachten Matrix-Schreibweise:
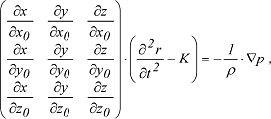 wobei ∇p=grad p= ∂p/∂k das Druckpotential ist. Die drei Gleichungen enthalten mit den Bahnkoordinaten (x, y, z) und dem Druck p vier Unbekannte, weshalb zur Lösung eine vierte Gleichung nötig ist. Dazu lässt sich das Kontinuitätsgesetz heranziehen. wobei ∇p=grad p= ∂p/∂k das Druckpotential ist. Die drei Gleichungen enthalten mit den Bahnkoordinaten (x, y, z) und dem Druck p vier Unbekannte, weshalb zur Lösung eine vierte Gleichung nötig ist. Dazu lässt sich das Kontinuitätsgesetz heranziehen. |
|