| |
Darstellung eines totalsymmetrischen Tensors s-ter Stufe durch eine Fläche s-ten Grades. Die Tensorfläche wird durch die Gleichung:
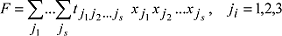 beschrieben. tj1j2...js sind die Tensorkomponenten, xj die Komponenten eines Ortsvektors. Zur Veranschaulichung soll die Fläche 2. Grades eines symmetrischen Tensors 2. Stufe diskutiert werden. Dann lautet die quadratische Form mit den sechs unabhängigen Tensorkomponenten: beschrieben. tj1j2...js sind die Tensorkomponenten, xj die Komponenten eines Ortsvektors. Zur Veranschaulichung soll die Fläche 2. Grades eines symmetrischen Tensors 2. Stufe diskutiert werden. Dann lautet die quadratische Form mit den sechs unabhängigen Tensorkomponenten:
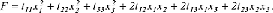 Gehen die Koordinatenachsen des Bezugssystems durch die Hauptachsen der Tensorfläche, was man durch eine sog. Hauptachsentransformation immer erreichen kann, so reduziert sich die Beziehung zu: Gehen die Koordinatenachsen des Bezugssystems durch die Hauptachsen der Tensorfläche, was man durch eine sog. Hauptachsentransformation immer erreichen kann, so reduziert sich die Beziehung zu:
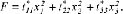 Der Vergleich mit der üblichen Beschreibung einer Fläche 2. Grades im Hauptachsensystem, nämlich: Der Vergleich mit der üblichen Beschreibung einer Fläche 2. Grades im Hauptachsensystem, nämlich:
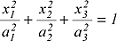 liefert folgende Beziehungen zwischen den Tensorkomponenten und den Halbachsen a1,a2,a3 der Tensorfläche: liefert folgende Beziehungen zwischen den Tensorkomponenten und den Halbachsen a1,a2,a3 der Tensorfläche:
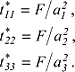 Sind die Tensorkomponenten alle positiv, so ist die Fläche 2. Grades ein allgemeines Ellipsoid mit den Halbachsen: Sind die Tensorkomponenten alle positiv, so ist die Fläche 2. Grades ein allgemeines Ellipsoid mit den Halbachsen:
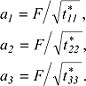 Für das tetragonale, trigonale und hexagonale Kristallsystem gilt: t*11=t*22; die Tensorfläche ist also Für das tetragonale, trigonale und hexagonale Kristallsystem gilt: t*11=t*22; die Tensorfläche ist also
ein Rotationsellipsoid. Im kubischen Kristallsystem mit t*11=t*22=t*33 ist die Tensorfläche eine Kugel.
Darauf beruht die Einführung der Indikatrix zur Beschreibung der anisotropen optischen Eigenschaften von Kristallen.
Die Tensorfläche erlaubt in Verbindung mit dem Grössenellipsoid den Effekt E zu der Einwirkung F
geometrisch nach Grösse und Richtung zu bestimmen. Das Grössenellipsoid wird für einen
symmetrischen Tensor 2. Stufe im Hauptachsensystem im allgemeinen durch:
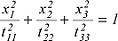 beschrieben. beschrieben.
Die Abbildung zeigt, wie zu der Einwirkung der Einheitsstärke F0=F/α der Effekt E0 zu bestimmen ist. Im Schnittpunkt von F0 mit der Tensorfläche wird der Flächennormalenvektor 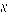
errichtet. Der Vektor parallel zu 
ausgehend vom Ursprung 0 gibt die Richtung des Effektes an, die Grösse des Effektes E0 ist bestimmt durch die Länge des Vektors vom Ursprung 0 bis zum Schnittpunkt mit Grössenellipsoid. Für die Einwirkung der Grösse F ergibt sich für E=αE0.
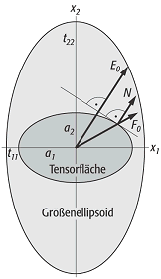 Tensorfläche: geometrische Bestimmung der Richtung und des Betrages eines Effektes mittels Tensorfläche und Grössenellipsoid (Schnitt durch die Achsen x1x2). Tensorfläche: geometrische Bestimmung der Richtung und des Betrages eines Effektes mittels Tensorfläche und Grössenellipsoid (Schnitt durch die Achsen x1x2). |
|